Matrix Chain Multiplication In Data Structure And Algorithm
Matrix Chain Multiplication Dynamic Programming Data Structure Algorithms If a chain of matrices is given we have to find the minimum number of the correct sequence of matrices to multiply. So there is only one way to multiply the matrices cost of which is 102030.
Matrix Chain Multiplication
Return C D 5.
Matrix chain multiplication in data structure and algorithm. P 10 20 30 Output. Eg if we have the cost for A1 A2 A3 is. Public static int solveIterative int s.
A poor choice of parenthesisation can be expensive. It is easy to see that this data structure is not space efficient if the matrix contains segments of adjacent nonzero elements since. The important point is that when we use the equation to calculate we must have already evaluated and For both cases the corresponding length of the matrix-chain are both less than.
Matrix Chain Multiplication using Dynamic Programming FormulaPATREON. MatrixMultiply A B. An Matrix multiplication is associative so A1 A2 A3 A1 A2 A3 that is we can can generate the product in two ways.
The cost of multiplying an n x m by an m x p one is O nmp or O n3 for two n x n ones. To watch the solution video click here. Int n slength - 1.
Matrix chain multiplication or Matrix Chain Ordering Problem MCOP is an optimization problem that can be solved using dynamic programming. Only defined for. Do j i l -1 7.
We know that the matrix multiplication is associative so four matrices ABCD we can multiply A BCD AB CD ABCD A BCD in these sequences. Do q m i k m k 1 j p i-1 p k p j 10. Given a sequence of matrices the goal is to find the most efficient way to multiply these matrices.
The minimum number of multiplications are obtained by putting parenthesis in following way ABCD -- 102030 103040 104030 Input. Let the input 4 matrices be A B C and D. Int p new int n n.
For k i to j-1 9. Multiplication of an m x n matrix A with an n XP matrix B can be accomplished in tQptA mtB time where t A and t B are the number of nonzero elements in A and B respectively. Do for i 1 to n-l 1 6.
Assume dimension of A is m x n dimension of B is p x q Begin if n is not same as p then exit otherwise define C matrix as m x q for i in range 0 to m - 1 do for j in range 0 to q 1 do for k in range 0 to p do C i j C i j A i k A k j done done done End. Return A i ADS. Do m i i 0 4.
6000 There are only two matrices of dimensions 10x20 and 20x30. Mij 8. Return Rec-MultAs1n Algorithm Rec-MultAsij 1.
Number of ways for parenthesizing the matrices. Matrix Chain Multiplication Problem can be stated as find the optimal parenthesization of a chain of matrices to be multiplied such that the number of scalar multiplication is minimized. You are given an arrayarr of positive integers of length N which represents the dimensions of N-1 matrices such that the ith matrix is of dimension arri-1 x arri.
P 10 20 30 Output. Given a sequence of matrices the goal is to find the most efficient way to multiply these matrices. Public class MatrixChainMultiply.
Input Format A number N arr1 arr2. For i 1 to n 3. Knapsack Matrix Chain Multiplication LCS Transitive Closure Floyd-Warshall 1.
The problem is not actually to perform the multiplications but merely to decide the sequence of the matrix multiplications involved. Lects 12 and 13 slide 15. Matrix chain multiplication or Matrix Chain Ordering Problem MCOP is an optimization problem that can be solved using dynamic programming.
6000 There are only two matrices of dimensions 10x20 and 20x30. The minimum number of multiplications are obtained by putting parenthesis in following way ABCD -- 102030 103040 104030 Input. For l 2 to n l is the chain length 5.
Algorithms asymptotic notation of running time complexity space and. Developing a Dynamic Programming Algorithm Step 3. In this video we state the problem where we required to multiply two matrices using the concepts of 2d arrays.
Algorithm of Matrix Chain Multiplication MATRIX-CHAIN-ORDER p 1. Int m new int n n. If i.
There are very large numbers of ways of parenthesizing these matrices. For int len 2. You have to find the minimum number of multiplications needed to multiply the given chain of matrices.
Compute the value of an optimal solution in a bottom-up fashion. N integers Output Format.
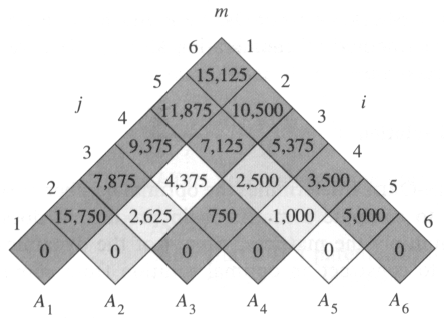
How To Solve Matrix Chain Multiplication Using Dynamic Programming Algorithms Blockchain And Cloud
4 3 Matrix Chain Multiplication Dynamic Programming Youtube
Matrix Chain Multiplication Problem Using Dynamic Programming Part 1 Youtube
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube
Optimum Order For Matrix Chain Multiplications Prismoskills
Massive Algorithms Matrix Chain Multiplication
Solved Consider The Matrix Chain Multiplication Problem T Chegg Com
Dynamic Programming 3 Example Matrix Chain Multiplication N N What If We Want To Multiply A String Of More Than Two Matrices Together Matrix Course Hero
Matrix Chain Multiplication Different Recursive Definition Stack Overflow
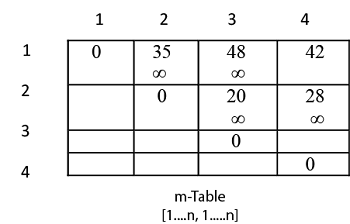
Matrix Chain Multiplication Algorithm Javatpoint
Matrix Chain Multiplication Problem Using Dynamic Programming Part 1 Youtube
Massive Algorithms Matrix Chain Multiplication
Matrix Chain Multiplication Geeksforgeeks Youtube
Matrix Chain Multiplication Dynamic Programming Youtube
Matrix Chain Multiplication
Matrix Chain Multiplication
Matrix Chain Multiplication
Matrix Multiplicationdesign
Matrix Chain Multiplication Dp 8 Tutorialspoint Dev
