Matrix Vector Product Mathematica
In general Cross v 1 v 2 v n - 1 is a totally antisymmetric product which takes vectors of length n and yields a vector of length n that is orthogonal to all of the v i. Cross v 1 v 2 gives the dual Hodge star of the wedge product.
Solve the general linear matrix equation a 1.
Matrix vector product mathematica. B m c for matrix by using the flattening vectorizing relation Flatten a. Home Embed All Linear Algebra Resources. The i j t h element is d f i d x j.
Product of a matrix and a vector. Let us define the multiplication between a matrix A and a vector x in which the number of columns in A equals the number of rows in x. In addition we define d f d x d f d x as the gradient matrix.
MrWs answered your problem but just to clarify. S is a differentiation matrix approximating the second derivative in 1 dimension. However we can specify either row-vector or column-vector and multiply by a matrix from left or right.
If we let A x b then b is an m 1 column vector. If possible Mathematica also conforms the vectors as needed. Simon Feb 4 12 at 1225.
Let i be a unit vector pointing east j be a unit vector pointing north and k be a unit vector pointing up. The latter uses mixed shifted and zero-shift iterations for high accuracy. Applying Dotto a rank tensor and a rank tensor gives a rank tensor.
Compute answers using Wolframs breakthrough technology knowledgebase relied on by millions of students professionals. Then the outer product that youre looking for is just matrix multiplication. For example a nxm matrix can multiply a m-wide row vector without objection.
I was wondering if there is an inbuilt Mathematica function that can take a vector v whose components are sums of variables x 1 x 2. B a b. Lanczos process requires one matrix-vector product evaluation with A 0.
M11m12m21m22n11n12n21n22 product of two matrices. See eg Section 51. 65F15 15A23 15A18 15B10 65G50.
Learn how to use Vectors and Matrices in Mathematica. CrossProduct v1 v2 coordsys gives the cross product of. B 1 a m.
Just like for the matrix-vector product the product A B between matrices A and B is defined only if the number of. Now we need to get the matrix into reduced echelon form. CrossProduct v1 v2 gives the cross product of the two 3-vectors v1 v2 in the default coordinate system.
For example is there a Mathematica function F such that. Orthogonal matrix to a condensed product form and an algorithm for full CS decomposition. So if A is an m n matrix then the product A x is defined for n 1 column vectors x.
This can be reduced to This is in equation form is which can be rewritten as. Now we need to substitute into or matrix in order to find the eigenvectors. The Wolfram Languages matrix operations handle both numeric and symbolic matrices automatically accessing large numbers of highly efficient algorithms.
CREATE AN ACCOUNT Create Tests Flashcards. A column vector is a 1n matrix and a row vector is a n1 matrix. When the vector is multiplied by a matrix from the right Mathematica treats the same vector as a row-vector.
V 21-1 row-vector u 2 1 -1 column-vector. When the spectral factorization of the reduction of A 0 is available the restoration of an image. Since we view vectors as column matrices the matrix-vector product is simply a special case of the matrix-matrix product ie a product between two matrices.
Cross x y gives the perpendicular vector - y x. The result of applying Dotto two tensors and is the tensor. Typically A 0 has a structure such as block Toeplitz with Toeplitz blocks that allows the evaluation of each matrix-vector product in only Onlogn ops.
For math science nutrition history. Unit vectors are non-denominate have a magnitude of unity and are used only to specify a direction Then the total vector in terms of its scalar components and the unit vectors can be written as V ai bj ck. As of Version 90 vector analysis functionality is built into the Wolfram Language.
Numerical examples are presented. Flatten x. We need to take the dot product and set it equal to zero and pick a value for and.
In vector form it looks like. 4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept. We define d f d x as the Jacobian of such function ie.
In Mathematica the dot operator is overloaded and can be matrix multiplication matrix-vector multiplicationvector-matrix multiplication or the scalar dot product of vectors depending on context. Here v vT. X n and turn it into a matrix-vector product where the matrix is just a coefficient matrix and vector is right and composed only of the variables.
The Wolfram Language uses state-of-the-art algorithms to work with both dense and sparse matrices and incorporates a number of powerful original algorithms especially for high-precision and symbolic matrices. The outer product u v is equivalent to a matrix multiplication uv or uvT if vectors are real provided that u is represented as a column m 1 vector and v as a column n 1 vector. Let f f 1 f 2 f n be a column vector function and x x 1 x 2 x n.
Matrix-Vector Product Study concepts example questions explanations for Linear Algebra. Orthogonal matrix Eigenvalue problem Full CS decomposition High accuracy AMS subject classi cation.

Pin On Geometry Theorems And Problems Math
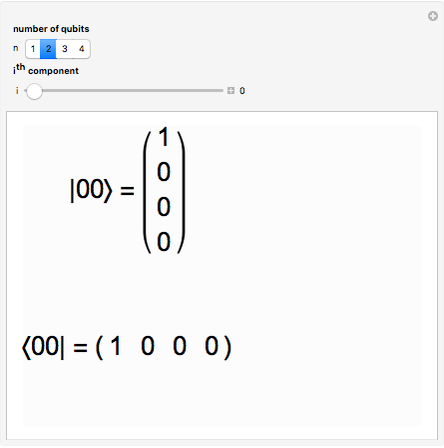
Quantum Computational Basis Vectors Wolfram Demonstrations Project

Through A Culturally Responsive Approach That Includes Methods Informed By Community Based Participatory Research We Work Tribal Community Brainstorming Icon

The Dot Operator Vs Standard Matrix Multiplication Online Technical Discussion Groups Wolfram Community

How To Get The Result Of A Multiplication Between A Matrix And A Vector Online Technical Discussion Groups Wolfram Community

The Vector Cross Product Youtube

3 4 1 Matrix Vector Multiplication Via Dot Product Youtube

Matrix Multiplication Wolfram Demonstrations Project

Is There Wolfram Alpha Syntax For Matrix Or Vector Calculus Quora

How To Calculate A Matrix Formed By Vector In Mathematica Stack Overflow

Solving Vector Equations In Mathematica Stack Overflow

The Vector Cross Product Youtube
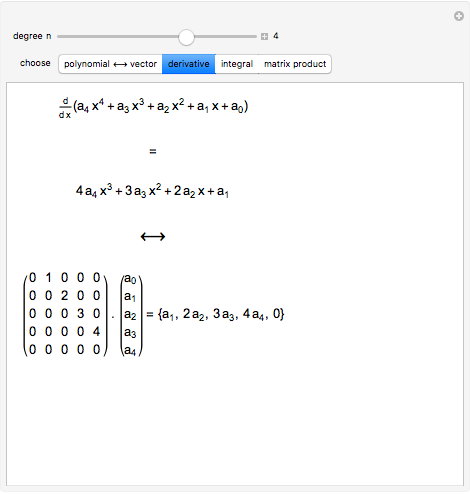
The Derivative And The Integral As Infinite Matrices Wolfram Demonstrations Project
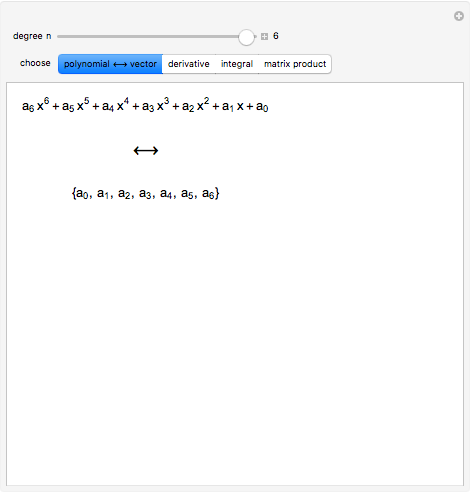
The Derivative And The Integral As Infinite Matrices Wolfram Demonstrations Project
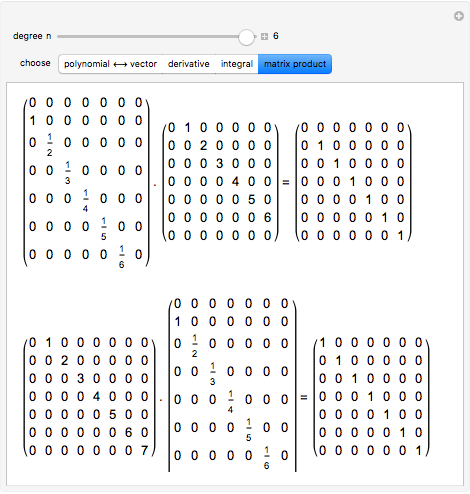
The Derivative And The Integral As Infinite Matrices Wolfram Demonstrations Project

Pin On Mechanics And Engineering


