+19 Dot Product Ideas

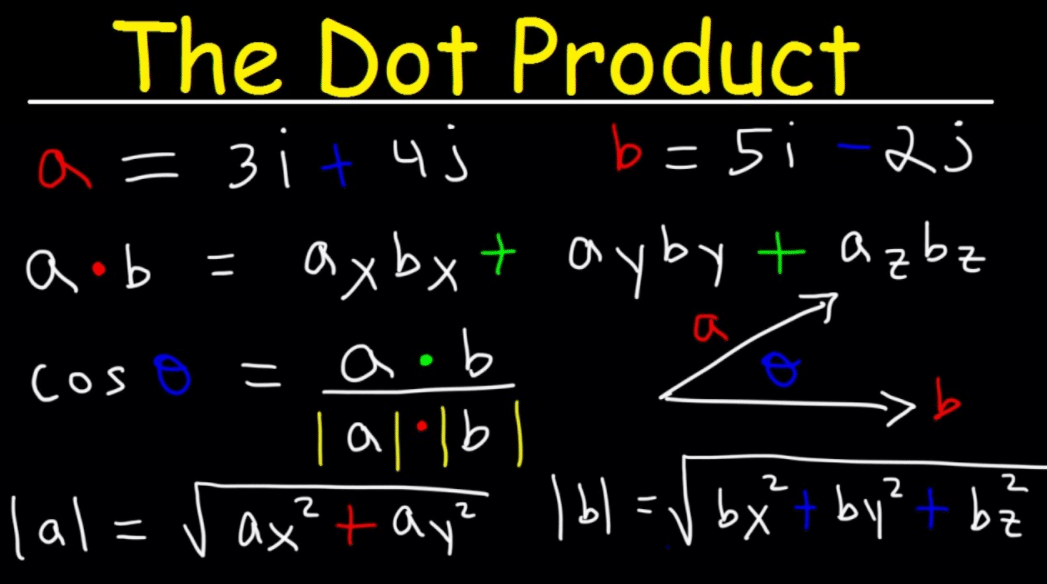
+19 Dot Product Ideas. Dot products are a particularly useful tool which can be used to compute the magnitude of a vector, determine the angle between two vectors, and find the rectangular. We write the dot product with a little dot between the two vectors (pronounced a dot b):

The Dot Product and Vectors Definition & Formula from theeducationtraining.com

The dot product essentially tells us how much of the force vector is applied in the direction of the motion vector. The dot product can be either a positive or negative real value. Given that the vectors are all of length one, the dot products are i⋅i.

Source: theeducationtraining.com

We can calculate the dot product of two vectors this way: If a.b = 0 then it can be clearly seen that either b or a is zero or cos θ.

Source: medium.com

These are the magnitudes of and , so. Dot products are a particularly useful tool which can be used to compute the magnitude of a vector, determine the angle between two vectors, and find the rectangular.

Source: www.onlinemathlearning.com

The dot product is written using a central dot: In linear algebra, a dot product is the result of multiplying the individual numerical values in two or more vectors.

Source: rehangetwin.blogspot.com

In this case, the angle is zero, and cos θ = 1 as θ = 0. Dot product properties of vector:

Source: www.slideserve.com

The dot product of two scalars is obtained by simply. In linear algebra, a dot product is the result of multiplying the individual numerical values in two or more vectors.

Source: www.youtube.com

Dot products are a particularly useful tool which can be used to compute the magnitude of a vector, determine the angle between two vectors, and find the rectangular. The dot product is a special case of the inner product that is limited to the real number space.

Source: gregorygundersen.com

Dot product determines the similarity between the two selected values for calculation and not the difference between them like the cross product. We write the dot product with a little dot between the two vectors (pronounced a dot b):

Source: datahacker.rs

In this example, we will take two scalar values, and print their dot product using numpy.dot (). We can calculate the dot product of two vectors this way:

Source: www.youtube.com

The dot product between a unit vector and itself can be easily computed. If we defined vector a as and vector b as <b 1, b 2, b 3.

A Dot Product Takes Two Vectors As Inputs And Combines Them In A Way That Returns A Single Number (A Scalar).

This means the dot product of a and b. The dot product, appropriately named for the raised dot signifying multiplication of two vectors, is a real number, not a vector. Dot product determines the similarity between the two selected values for calculation and not the difference between them like the cross product.

If We Defined Vector A As And Vector B As <B 1, B 2, B 3.

The dot product can be either a positive or negative real value. If we break this down factor by factor, the first two are and. Two vectors are orthogonal only if a.b=0.

The Dot Product Between A Unit Vector And Itself Can Be Easily Computed.

And that is why the dot product is sometimes. In linear algebra, a dot product is the result of multiplying the individual numerical values in two or more vectors. In this example, we will take two scalar values, and print their dot product using numpy.dot ().

Therefore, It Can Be Both Positive And Negative.

A · b = | a | × | b | × cos (θ) where: Besides, it usually doesn’t even go by the name if a dot product, but rather. The dot product further assists in measuring the angle created by a combination of vectors and also aids in finding the position of a vector concerning the coordinate axis.

The Dot Product Is A Special Case Of The Inner Product That Is Limited To The Real Number Space.

If α is 90° then scalar product is zero as cos (90) = 0. Scalar product is commutative i.e. The dot product can also help us measure the angle formed by.