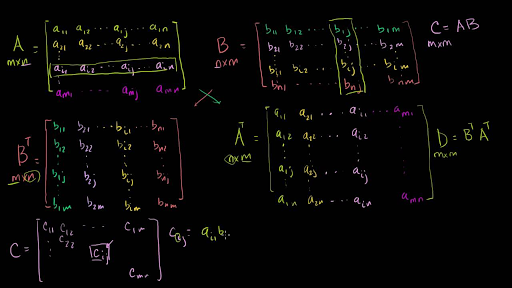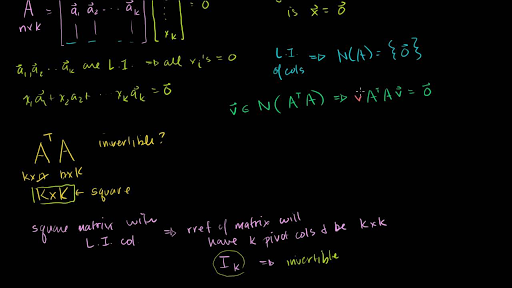Matrix Times Transpose Positive Definite

30 Aug, 2021

Transpose of a matrix triangular matrix triangular factorization. N are all groups with respect to the usual matrix multiplication.

Http Nitro Biosci Arizona Edu Workshops Mm2012 Notes Pdfs Lecture01 Matrix Pdf

In other words it also satisfies property HIP3.

Matrix times transpose positive definite. Positive definite Real Symmetric Matrix and its Eigenvalues A real symmetric n times n matrix A is called positive definite if mathbfxtransAmathbfx0 for all nonzero vectors mathbfx in Rn. In particular we need because the rank is at most the number of columns as well as at most the number of rows. Did you know that for any matrix the matrix is positive semidefinite PSD.

Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as ﬂipping entries about the diagonal. A Prove that the eigenvalues of a real symmetric positive-definite matrix A are all positive. 1 For a positive definite integral symmetric matrix S of rank S 7 Or When rank S 8 S has an odd entry in its diagonal there is an integral matrix satisfying Mt S if there is a rational matrix R with RN S.

A short summary of Cholesky decomposition. Ask Question Asked 5 years 8 months ago. What I meant by absolute minima we achieved minima at all axis.

A Hermitian inner product on C n is a conjugate-symmetric sesquilinear pairing P that is also positive definite. If in addition A Rnn A R n n then A A is said to be symmetric positive definite SPD. Deﬁnition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Deﬁnition A square matrix A is symmetric if AT A.

1 D n P n D n. When my S is A transpose A thats my S. For any non-zero vector x.

Here you go with a geometric interpretation. That -- take -- weve looked at products of three guys like that and taken their transpose and we got it back again. XTX is always positive semidefinite.

If a matrix is positive semi-definite It has a minima in at least one axis vector. It also follows immediately by considering transposes that every is PSD. An orthogonal matrix times diagonal times the transpose of that orthogonal matrix.

The following two results are proved. Why this property positive semi-definite is critical in machine learning. Therefore x A x 0 when x 0.

X H A x 0. U n L n D n. Active 4 years ago.

If you can generate a random matrix in your chosen language then by using the property that a matrix multiplied by its transpose is positive semi-definte you can generate a random positive semi-definite matix. Then if H and V are any two positive definite matrices Aµ is another because xTA. Viewed 24k times 26.

Associativity of addition and multiplication basis bases change of basis canonical form under Congruences E T1 AE. At this point. Im OK with equation 2.

But now I look at this. Endgroup Wolfgang Bangerth Mar 12 16 at 1754. Related section in textbook.

6 The transpose of orthogonal matrix A is also orthogonal 7 The inverse of from DATA 12 at Deakin University. Ie AT ij A ji ij. A positive definite matrix has positive eigenvalues positive pivots positive determinants and positive energy.

Spectral theorem for RSMs and positive definiteness Here are two simple observations. The only element of D n that equals is its own inverse is the identity. Since x A x is a scalar we know that x A x x A x x A x.

Times the first row to the second row. Try for example with a matrix that has a zero column or is in fact entirely composed of zeros. Then I have x transpose times the left side is x transpose times the right side.

The same holds for matrices over the complex numbers provided you use the Hermitian transpose rather than the transpose. By the definition of positive definite the positive definite matrix A has the property that x A x 0 when x 0. Second the nxn matrix A is called positive semi-definite if x A xt 0 for any non-zero vector x.

Posted on January 31 2018. Given the real matrix the matrix is positive definite if and only if the rank of is equal to. And of course everybody immediately says yes and if this is possible then thats clearly symmetric right.

Therefore the transpose of the positive definite matrix A is positive definite. It can be positive semidefinite. A matrix A Cnn A C n n is Hermitian positive definite HPD if and only if it is Hermitian AH A A H A and for all nonzero vectors x Cn x C n it is the case that xHAx 0.

Is a positive definite matrix times a positive semidefinite matrix positive semidefinite. P v v 0 iff v 0. Begingroup As a small remark the product of a matrix and its transpose doesnt have to be positive definite.

P v v 0. Every symmetric positive definite matrix M can be decomposed into a product of a unique lower triangular matrix L and its transpose LT. If a matrix is positive definite It has an absolute minima minima.

For this reason we call a Hermitian matrix positive definite iff all of its eigenvalues which are real numbers are positive. For any vector Note that this applies for real matrices of any size. Monte-Carlo methods are ideal for option pricing where the payoff is dependent on a basket of underlying assets For a basket of n assets the correlation matrix Σ is symmetric and positive definite therefore it can be factorized as Σ LLT where L is a lower triangular matrix.

The transpose map sets up an anti-isomorphism between the groups U n and L n. Proof for why a matrix multiplied by its transpose is positive semidefinite. The proof is literally one-line.

In Matlab it would be as simple as Generate a random 3x3 matrix A rand33 Multiply by its tranpose PosSemDef AA.

Linear Algebra Ppt Download

Summary Of Matrix Manipulations

Appendix A Review Of Linear Algebra Appendix B

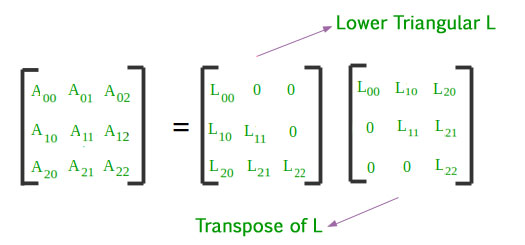
Cholesky Decomposition Matrix Decomposition Geeksforgeeks

Engineering And Scientific Subroutine Library For Aix Version 3 Release 3 Guide And Reference Matrices

How To Prove That The Transpose Of The Identity Matrix Does Not Change The Matrix Quora

Summary Of Matrix Manipulations

What S The Meaning Of Matrix S Transpose Multiplied By The Matrix Itself Quora

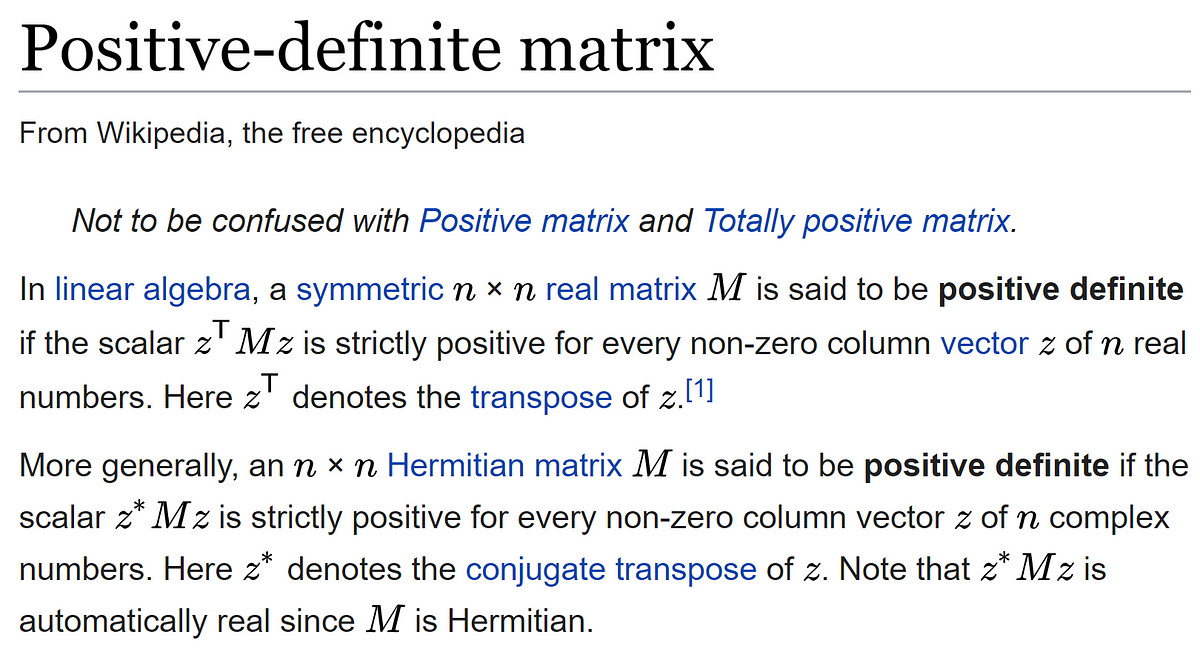
What Is A Positive Definite Matrix By Aerin Kim Towards Data Science

7 Linear Algebra Matrices Vectors Determinants Linear Systems Ppt Download

Will The Product Of A Real Valued Matrix And Its Transpose Always Have A Real Eigenvector Mathematics Stack Exchange

Transpose Of A Matrix Product Video Khan Academy

Matrix Definitions It Is Assumed You Are Already Familiar With The Terms Matrix Matrix Transpose Vector Row Vector Column Vector Unit Vector Zero Ppt Download