Matrix Multiplication Pseudocode
Source code for matrix multiplication using the text file. Result valve.
Matrix Multiplication With A Hypercube Algorithm On Multi Core Processor Cluster
End array S 1.

Matrix multiplication pseudocode. M i j cost. If cost m i j. The above strategy is the basic O N3 strategy.
Using the Master Theorem with T n 8T n2 O n2 we still get a runtime of O n3. Recursive code for Matrix Multiplication include const int MAX 100. For k i to j-1 9.
K is used to know current column number of A and row number of B to be multiplied static int i 0 j 0 k 0. The Steps in Pseudo code. If alen 0 return vec.
Let the input 4 matrices be A B C and D. This pseudocode contains the algorithm for matrix multiplication only. C11 A11B11 A12B21 C12 A11B12 A12B22 C21 A21B11 A22B21 C22 A21B12 A22B22 The First Attempt Straightforward from the formulas above assuming that n is a power of 2.
ConsoleWriteLinetodoublepenetration the elements of Matrix. Algorithm of Matrix Chain Multiplication MATRIX-CHAIN-ORDER p 1. The unit of computation of of matrix A B is one element in the matrix.
For l 2 to n l is the chain length 5. For problems or questions regarding this web page contact muralircsrutgersedu. Begin array ll S_1 6 S_6 8 S_2 4 S_7 -2 S_3 12 S_8 6 S_4 -2 S_9 -6 S_5 6 S_ 10 14.
Cost m i k m k1 j dims i-1dims kdims j. Else if b 0len 0 return vec. The input information of the.
Do for i 1 to n-l 1 6. Square matrix multiplication pseudocode. MatrixMultiply A B.
A faithful translation of these nested loops into Rust looks like this. For i 1 to n 3. For small-to-medium-sized dense matrices I believe that some variation on the naive ON3 algorithm is a win if you pay attention to cache-coherence and use the platforms vector instructions.
Vec - Vec if blen 0 return vec. Strassens insight was that we dont actually need 8 recursive calls to complete this process. Loop Multiply Components of Matrix A by Components of Matrix B.
S 1 6 S 6 8 S 2 4 S 7 2 S 3 1 2 S 8 6 S 4 2 S 9 6 S 5 6 S 1 0 1 4. How to read and write data can be found in the source code below. Loop Input Get User Defined Demensions of Matrix B.
Matrix C aebg afbh cedg cfdh. Loop Input Get User Defined Components of Matrix B. ClassToString int a.
L is length of chain product 5 do for i 1 to n l 1 6 do j i l 1 7 mi j inf 8 for k i to j 1 9 do q mi k mk1 j pi-1pk pj 10 if q mi j. Depends on the size of the matrix and whether its sparse or not. 30000 There are 4 matrices of dimensions 10x20 20x30 30x40 and 40x30.
Do q m i k m k 1 j p i-1 p k p j 10. . The final step in the MapReduce algorithm is to produce the matrix A B.
P 10 20 30 40 30 Output. Do j i l -1 7. The reduce step in the MapReduce Algorithm for matrix multiplication Facts.
Data arrangement is important -- for cases where your standard matrix layout is cache-unfriendly eg column-major row-major. Void multiplyMatrixRecint row1 int col1 int AMAX int row2 int col2 int BMAX int CMAX Note that below variables are static i and j are used to know current cell of result matrix C. Loop Output Results of Matrix AB.
Map key values for i k aij in valve. We will generate the matrix A and matrix B and write it to text file matrixAtxt and matrixBtxt respectively. Loop Input Get User Defined Components of Matrix A.
Else if a 0len 0 return vec. The first matrices are. Divide-and-Conquer algorithsm for matrix multiplication A A11 A12 A21 A22 B B11 B12 B21 B22 C AB C11 C12 C21 C22 Formulas for C11C12C21C22.
Pseudo-code for the algorithm is as follows. For valve in values. Sequentially multiply A and B square matrices.
Assume dimension of A is m x n dimension of B is p x q Begin if n is not same as p then exit otherwise define C matrix as m x q for i in range 0 to m - 1 do for j in range 0 to q 1 do for k in range 0 to p do C i j C i j A i k A k j done done done End. These two matrices text files will be the input to the main matrix multiplication. The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input.
The block diagram of two stage map reduce multiplication algorithm can be shown as follows. ConsoleWriten Enter the number of rows in Matrix 1. Index of the subsequence split that achieved minimal cost.
S i j k. As evident from the three nested for loops in the pseudocode above the complexity of this algorithm is On3. ConsoleWriten Enter the number of columns in Matrix 1.
Pseudocode Matrix-chain-order p. If n 1 Output AB 2. Program in C to multiply two matrices using Rectangular arrays.
Emit i aij v j reduce key values result 0. Public void ReadMatrix ConsoleWriteLinen Size of Matrix 1. P 1n lengthp 1 2for i 1 to n 3 do mi i 0 4for l 2 to n.
Mij 8. Do m i i 0 4. Loop Input Get User Defined Demensions of Matrix A.

An Optimized Floating Point Matrix Multiplication On Fpga Scialert Responsive Version

Pseudocode For The Matrix Multiplication Algorithm Download Scientific Diagram

Problem 2 The Multiprocessor Pseudocode For Chegg Com

Figure 1 From A Proposed Fpga Based Parallel Architecture For Matrix Multiplication Semantic Scholar

Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram

Let A And B Be Two N By N Matrices We Can Multiply Chegg Com

Ppt Matrix Multiplication Powerpoint Presentation Free Download Id 2231814

Figure 1 From Hardware Realization Of Matrix Multiplication Using Field Programmable Gate Array Semantic Scholar

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange
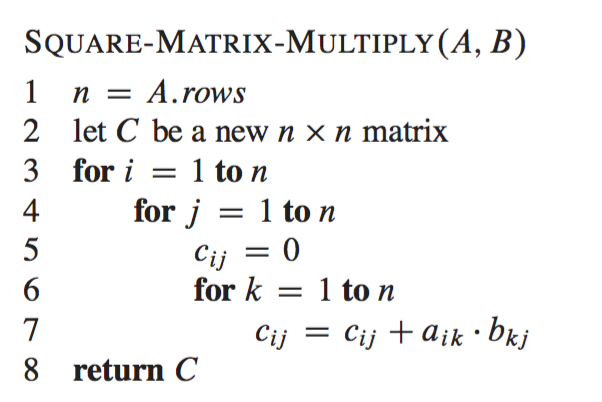
Matrix Multiplication Using The Divide And Conquer Paradigm

Solved Consider The Matrix Chain Multiplication Problem T Chegg Com

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Pseudocode For Matrix Multiplication Download Scientific Diagram

Square Matrix Multiply Recursive In Java Using Divide And Conquer Stack Overflow

In Java First Create A Chegg Com

Matrix Chain Multiplication Explained Kilichbek Haydarov

Pseudocode Of Matrix Multiplication Using Cannon S Algorithm Download Scientific Diagram
