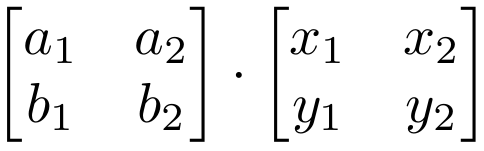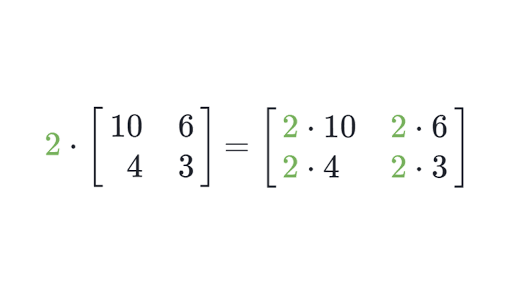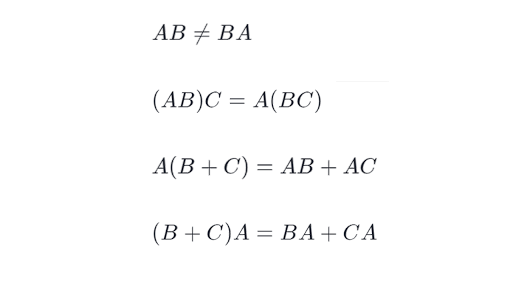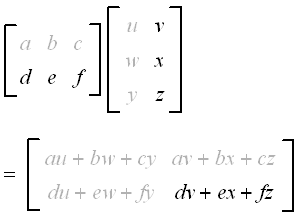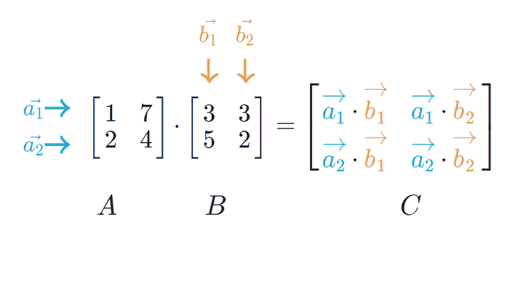Matrix Multiplication From Right To Left
What is obtained on the right is the inverse of the original matrix. 1 0 0-1 1 0-4 1 1 6.
15 3 Matrix Multiplication Chemistry Libretexts
And left-multiplying by a matrix is the same thing repeated for every result row.
Matrix multiplication from right to left. Matrix multiplication is defined so that it works right to left just like function composition. Multiplication of two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix. The examples in this article apply to active rotations of vectors counterclockwise in a right-handed coordinate system y counterclockwise from x by pre-multiplication R on the left.
It is E 2E 1A not E 1E 2A. But its confusing that a left-multiplication transformation is defined using a matrix and need the idea of matrix multiplication. Since I havent decided which are the two bases to be used to represent those x F.
Left-multiplying a matrix X by a row vector is a linear combination of Xs rows. It is a very important step. Its also why we conventionally represent vectors as column matrices.
Is represented graphically thus. Suppose we are given the matrices A and B find AB do matrix multiplication if applicable. Formally the i-th row j-th column element of A T is the j.
It becomes the linear combination of the rows of X with the coefficients taken from the rows of the matrix on the left. If you multiply from the left eg. Two matrices can only be multiplied if the number of columns of the matrix on the left is the same as the number of rows of the matrix on the right.
Write the rows of A as the columns of A T. If any one of these is changed such as rotating axes instead of vectors a passive transformation then the inverse of the example matrix should be used. With no parentheses the order of operations is left to right so AB is calculated first which forms a 500-by-500 matrix.
Use matrix multiplication to show that AA1 I A A 1 I and A1A I A 1 A I. A matrix with 2 columns can be multiplied by any matrix with 2 rows. Use elementary row operations so that the identity appears on the left.
Say I have matrix an existing transformation matrix mathbfM and then other. Due to the matrix multiplication rules not all matrices can be multiplied. Consider the case of multiplying three matrices with ABC where A is 500-by-2 B is 2-by-500 and C is 500-by-2.
This matrix is then multiplied with C to arrive at the 500-by-2 result. It depends if you transform your points by multiplying the matrix from the left or from the right. 2 x 3 times 3 x 3.
Lets say we have three matrices a B and C and lets say that B and C are both M by n matrices and that a is a lets call it a K by M matrix and what I want to do is figure out whether matrix products exhibit the distributive property so lets test out a times B plus C a times B plus C and of course these are all matrices so B just to make things clear be the matrix B could be represented as. I have seen that many composite transformations have the later transformation multiplied to the right side of the matrix. An easy way to determine this is to write out each matrixs rows x columns and if the numbers on the inside are the same they can be multiplied.
Determine which one is the left and right matrices based on their location. In order to make it clear whether you need a left or right multiplication it is important to highlight in which reference frame your. F n F m L A x A x for any x F n which is a left-multiplication transformation defined using a matrix A.
The transpose of a matrix A denoted by A T A A A A tr t A or A t may be constructed by any one of the following methods. This allows matrices to represent linear transformations more intuitively. Reflect A over its main diagonal which runs from top-left to bottom-right to obtain A T.
Write the original matrix augmented with the identity matrix on the right. Now lets examine left-multiplication. Ax x where A is a matrix and x the transformed point you just need to swap the second and third column.
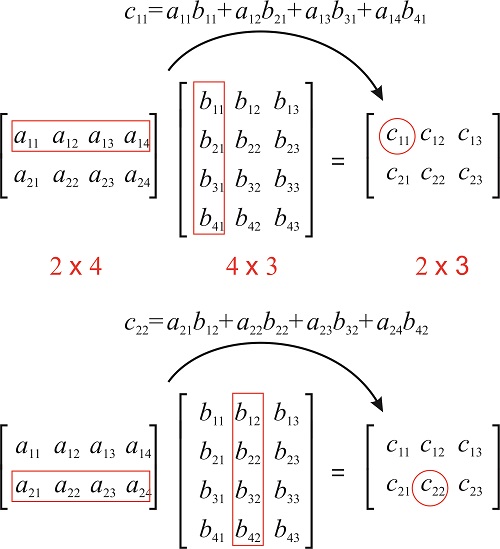
If A is an m -by- n matrix and B is an n -by- p matrix then their matrix product AB is the m -by- p matrix whose entries are given by dot product of the corresponding row of A and the. In order for matrix multiplication to work the number of columns of the left matrix MUST EQUAL to the number of rows of the right matrix. Write the columns of A as the rows of A T.
Notice that we multiplied A by the elimination matrices from right to left in the order of the steps. These matrices may be multiplied by each other to create a 2 x 3 matrix. Because matrix multiplication is generallynot commutative E 2E 1 and E 1E 2 give di erent matrices.
In 25E2E1 Out253 3 ArrayfInt642g.
Matrix Multiplication Calculator

Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
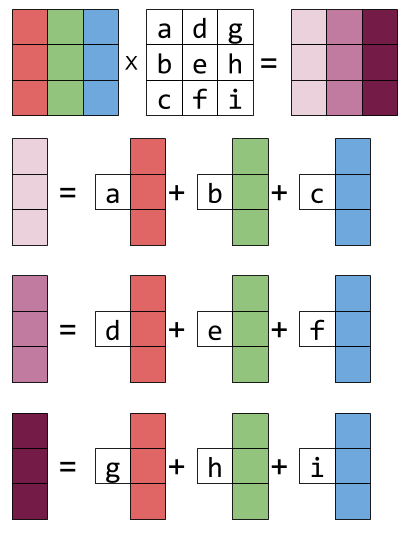
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Multiplying Matrices By Scalars Article Khan Academy
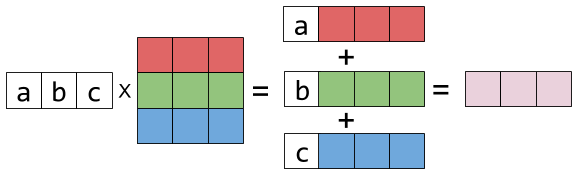
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Properties Of Matrix Multiplication Article Khan Academy

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
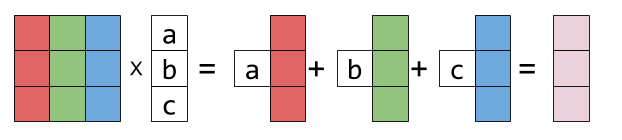
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Matrices And Matrix Calculations
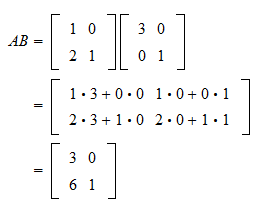
Matrix Multiplication And Linear Combinations
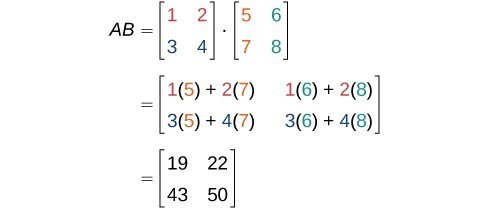
Finding The Product Of Two Matrices College Algebra
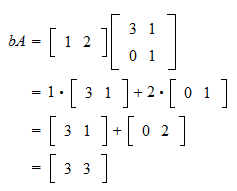
Matrix Multiplication And Linear Combinations
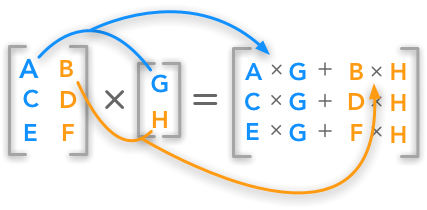
Introduction To Matrices And Vectors Multiplication Using Python Numpy
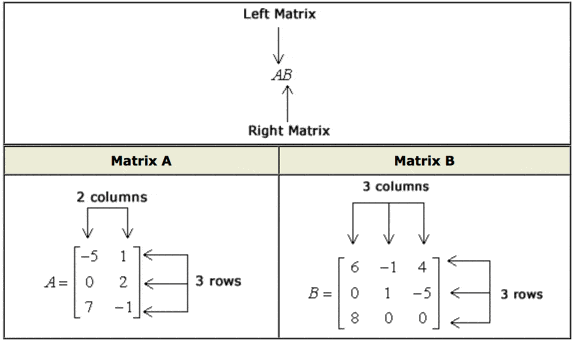
Matrix Multiplication Chilimath
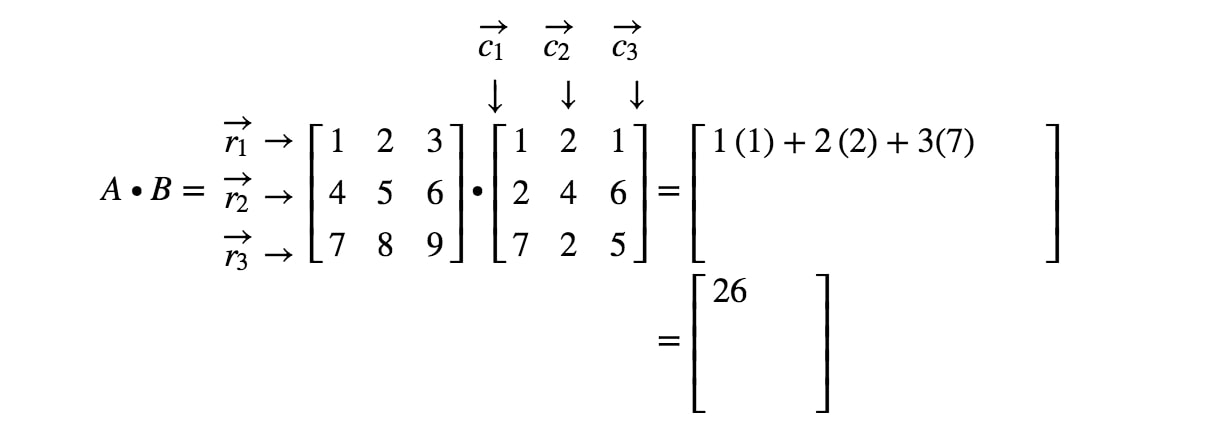
How To Multiply Two Matrices Together Studypug
Multiplying Matrices Article Matrices Khan Academy
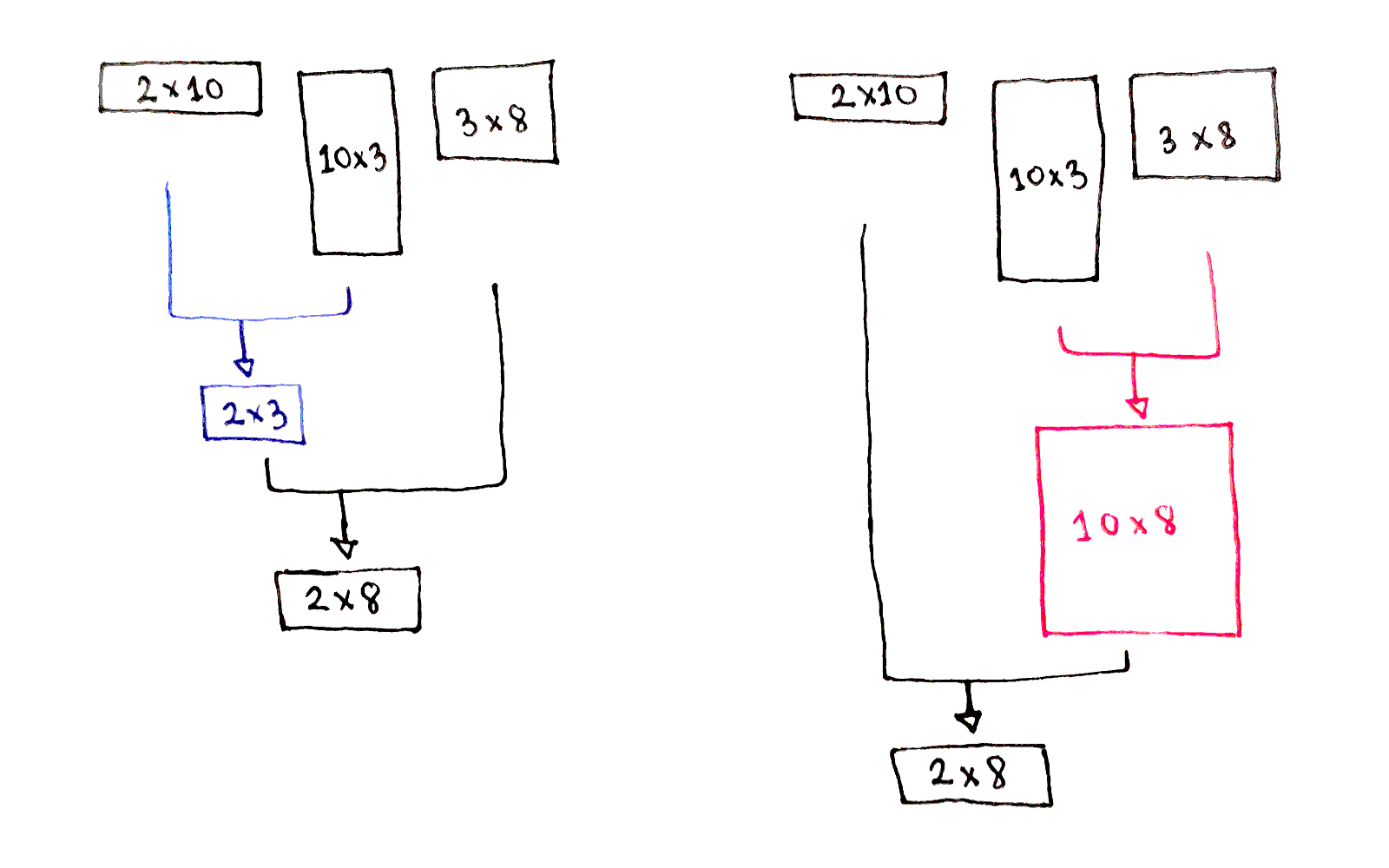
Dynamic Programming Deep Dive Chain Matrix Multiplication