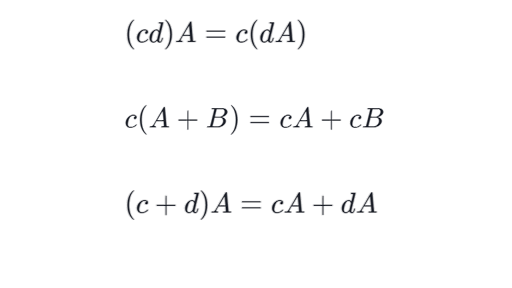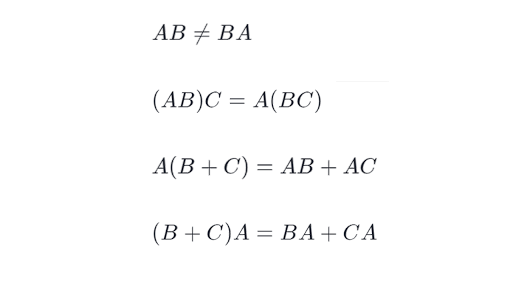Is Scalar Matrix Multiplication Commutative
For example this always works when Ais the zero matrix or when AB. You cannot switch the order of the factors and expect to end up with the same result.
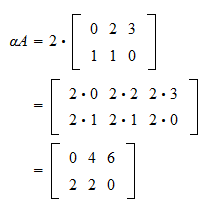
Multiplication Of A Matrix By A Scalar
X Y be the linear function with matrix N and g.
Is scalar matrix multiplication commutative. P A is an m n matrix. Matrix Multiplication is distributive across addition Note however that the order still does matter the above is not the same as The above is not true but the following is true Multiplying a scalar constant across matrix multiplication is commutative in the. Y Z be the linear function with matrix M.
A matrix is a rectangular array of numbers or other mathematical objects for which operations such as addition and multiplication are defined. Let A and B be m n matrices. The reader is encouraged to find other examples.
Of course if just want to say that it doesnt matter how you write the product λ v v λ where λ is a scalar and v is a vector then thats trivially true but that is not what commutative means. Yes its true and also easy to prove. While matrix multiplication is not commutative in general there are examples of matrices Aand Bwith ABBA.
You have for each vector x X. When pre-multiplying a matrix by a scalar a TypeError is raised. α M N x α g f x α g f x α g f x g is linear g α f x g α f x M α N x Share.
ExampleNon-commutative multiplication of matrices. Let O m n be the m n zero matrix and let p and q be scalars. YES When you mutliply a matrix by a scalar you multiply each element input of the matrix by the same scalar and we know that the multiplication in R or in C is commutative.
What you do know is that a matrix A commutes with A n for all n negative too if it is invertible and A 0 I so for every polynomial P or Laurent polynomial if A is invertible you have that A commutes. Scalar multiplication is the product of a scalar and a vector- you cant interchange them. Post-multiplication works as expected.
Most of this article focuses on real and complex matrices that is matrices whose elements are respectively real numbers or complex. Last edited by a moderator. Properties of Scalar Multiplication.
Most commonly a matrix over a field F is a rectangular array of scalars each of which is a member of F. P q A p q A. Properties of Scalar Multiplication.
In particular matrix multiplication is not commutative.
Pin On The Math Series Tpt Store For Secondary Math Teachers
Properties Of Matrix Scalar Multiplication Article Khan Academy
Pin On Math Education
3 4a Matrix Operations Finite Math
Pin On Math Classroom Activities
Introduction To Matrices Includes The Following Foldable Activities What Is A Matrix What Ar Matrices Math Interactive Notebook Activities Teaching Algebra
Multiplying A Matrix By A Scalar Properties Of Scalar Multiplication Youtube
How To Multiply Matrices By Scalars Studypug
Properties Of Matrix Multiplication Article Khan Academy
Pin On A School Resources
Theorem 2 1 Properties Of Matrix Addition And Scalar Chegg Com
Pin On Matrix
Multiplication Of Matrices Is The Operation Of Multiplying A Matrix Either With A Scalar Or By Another Matrix Matrix Multiplication Http Math Tutorvista Co
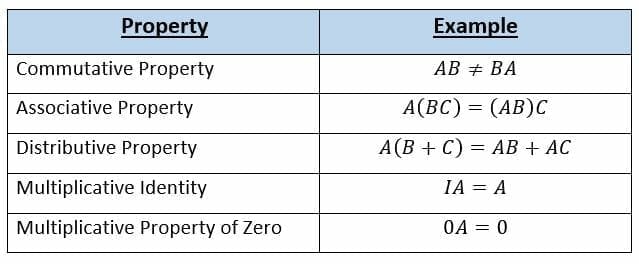
Matrix Multiplication Explanation Examples
Is Matrix Multiplication Commutative Video Khan Academy
Pin On Matrices And Linear Systems High School Math Classroom Resources
Pin On Students
Pin On Matrices Math
Matrices Foldable Matrices Math Math Interactive Notebook Algebra
