Invertible Matrices Identity Matrix
There are several methods and shortcuts to find the inverse of a Matrix. This can be derived using blockwise matrix inversion.
Determinants And Inverse Matrices Algebra 2 Help Matrix Precalculus
Just know that matrices are only properly invertible if they are square matrices.
Invertible matrices identity matrix. Determining invertible matrices. Division but its analogous to it so before we introduce that lets Im going to introduce you to the concept of an identity matrix so the identity matrix is a matrix and Ill denote that by capital I when I multiply it times. The definition of a matrix inverse requires commutativitythe multiplication must work the same in either order.
Let A and B be nxn matrices and let I be the nxn identity matrix. Viewed 66 times -1. The Woodbury matrix identity is where A U C and V are conformable matrices.
In particular the identity matrix serves as the multiplicative identity of the ring of all n n matrices and as the identity element of the general linear group GL n a group consisting of all invertible n n matrices. Active 7 months ago. When solving equations like 8x72 you can use the ERAA and multiply both sides of the equation by the multiplicative inverse of 8 to get x9.
The inverse of a Matrix Suppose A is a square matrix now this A matrix is known as invertible only in one condition if their another matrix B of the same dimension exists such that AB BA I n where I n is known as identity matrix of the same order and. Inverse Matrix The matrix which when multiplied by the original matrix gives the identity matrix as the solution. Invertible matrices are an important part of linear algebra.
We learned about matrix multiplication so what about matrix division. A is n n C is k k U is n k and V is k n. 18 8 1.
If we have an identity matrix no matter what row operations scalar multiplication or. But we can multiply a matrix by its inverse which is kind of. It is the matrix that results in the identity matrix when it is multiplied by A.
Invertible matrix and its inverse. To determine the inverse of the matrix 3 4 5 6 set 3 4 5 6a b c d 1 0 0 1. In fact we need only one of the two.
But I was wondering if the opposite is true ie. In the definition of an invertible matrix A we used both and to be equal to the identity matrix. A -1 A I.
1 begingroup I know that all invertible matrices can be row reduced to the identity matrix. If this is the. Invertible Matrices And Identity Matrix.
If I AB is invertible show that I BA is also invertible and that I BA-1 1 BI AB-1 A Question. A A -1 I. A 1A In This means that if we apply a linear transformation to the space with A it is possible to go back with A 1.
When we multiply a number by its reciprocal we get 1. Same thing when the inverse comes first. To be invertible a matrix must be square because the identity matrix must be square as well.
Inverse Matrix Calculator usually adopts Gauss-Jordan also known as Elementary Row Operations method and Adjoint method to perform the intended function. The matrix inverse of A is denoted A 1. Ask Question Asked 7 months ago.
There is no such thing. So there is no pair of 2x3 and 3x2 matrices that multiply to an identity matrix in both directions. If B exists it is unique and is called the inverse matrix of A denoted A 1.
While the identity is primarily used on matrices it holds in a general ring or in an Ab-category. Let A and B be nxn matrices and let I be the nxn identity matrix. Sal introduces the concept of an inverse matrix.
In particular the identity matrix is invertiblewith its inverse being precisely itself. When we multiply a matrix by its inverse we get the Identity Matrix which is like 1 for matrices. Inverse Matrix Calculator is a mathematical tool that performs all the lengthy and tricky calculations in seconds to find the Inverse of a given Matrix.
In other words for a matrix A if there exists a matrix Bsuch that then Ais invertible and B A-1. A square matrix A is called invertible or non-singular if there exists a matrix B such that AB BA I n where I n is the nn identity matrix with 1s on the main diagonal and 0s elsewhere. 8 18 1.
Invertible matrix 1 Invertible matrix In linear algebra an n-by-n square matrix A is called invertible or nonsingular or nondegenerate if there exists an n-by-n matrix B such that where I n denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication.
Pin On Matrices Math
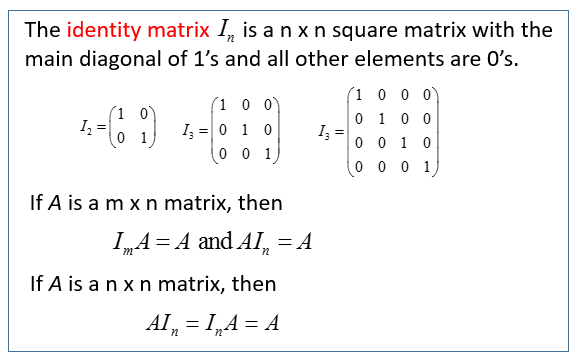
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities
Pin On Matrices Math
Invertible Matrix Definition Deepai
Linear Programming Lesson Algebra Lesson Plans Linear Programming Algebra Lessons
Foldable To Organize The Algebraic And Matrices Rules For Translations Reflections Rotations And Dilations T Geometry Lessons Matrices Math Math Classroom
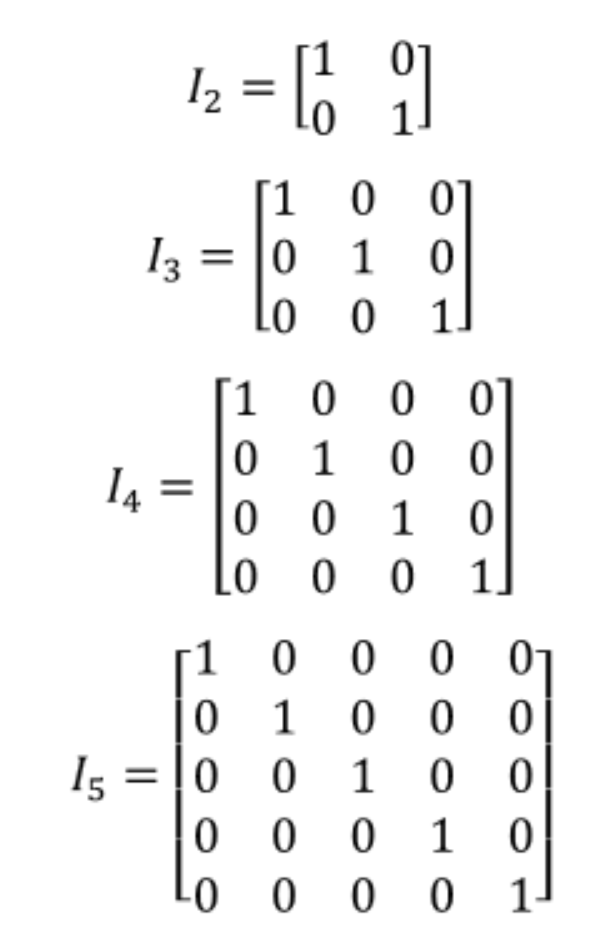
What Is An Identity Matrix Studypug
Pin On Math Resources
Matrix Word Problems Multiplying Matrices
Inverse Matrices And Their Properties Youtube
Pin On Math Resources
Identity Matrix And Proving Inverse Matrices Youtube
Why Can All Invertible Matrices Be Row Reduced To The Identity Matrix Mathematics Stack Exchange
Matrix Inverse Matrices Math Math Lessons Math
Pin On Secondary Math And More
Misconceptions When Multiply 2 Matrices The First Matrix S Column Needs To Match The Value Of The Second Matrix S Row In O Matrices Math The One Matrix Matrix
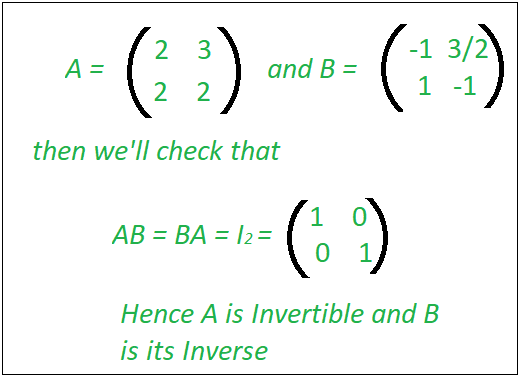
Check If A Matrix Is Invertible Geeksforgeeks
Pin On Matrices Math
Pin Auf Matho