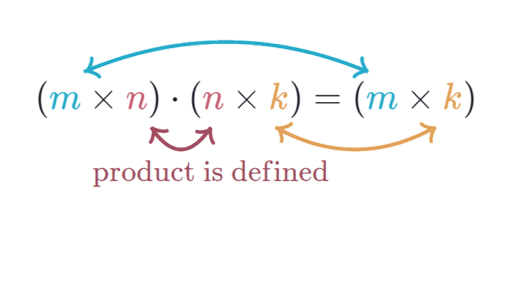What Is The Complexity Of Matrix Multiplication Operations Explain In Brief
It was the first algorithm to. The time complexity is ON 28074.
Introduction To Matrices And Matrix Arithmetic For Machine Learning
It can be optimized using Strassens Matrix Multiplication.
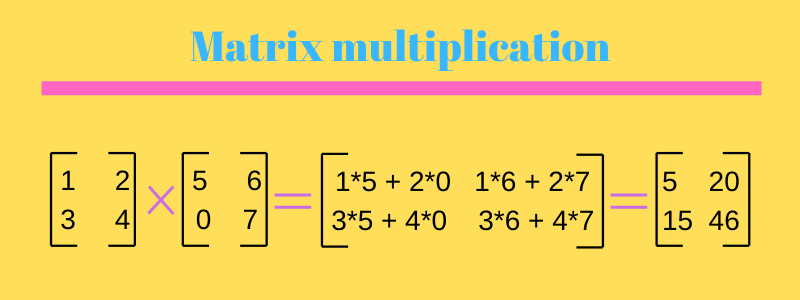
What is the complexity of matrix multiplication operations explain in brief. In general for 1 i p and 1 j r. These nine separate calculations have been done using very few lines of code involving loops and function in this C program for Matrix Multiplication. Note that has entries and each entry takes time to compute so the total procedure takes time.
It means the matrices are 1 x 2 2 x 3 3 x 4. On 2 Multiplication of Rectangular Matrices. 30000 There are 4.
Minimum number of operations need multiply these three matrices. Algorithm matOrderarray n Input List of matrices the number of matrices in the list. We use pointers in C to multiply to matrices.
For example if A is a 10 30 matrix B is a 30 5 matrix and C is a 5 60 matrix then computing ABC needs 1500 3000 4500 operations while computing A needs 9000 18000 27000 operations. 15125 Time Complexity for Matrix Chain Multiplication. Minimum number of operation used are.
Using this recurrence relation we get T n O n l o g 7 Hence the complexity of Strassens matrix multiplication algorithm is O n l o g 7. 6 2 8 7 The first matrix is 5 6 1 7 The second matrix is 6 2 8 7 After multiplication 78 52 62 51 Complexity. In general multipling two matrices of size N X N takes N3 operations.
5 6 1 7 Enter the 4 element of second matrix. The matrix multiplication takes place as shown below and this same procedure is is used for multiplication of matrices using C. P 10 20 30 40 30 Output.
Volker Strassen first published his algorithm in 1969. Here the result is 18. The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input.
The number of multiplications needed are. Enter the 4 elements of first matrix. By this we mean that we have to follow the above matrix order for multiplication but we are free to parenthesize the above multiplication depending upon our need.
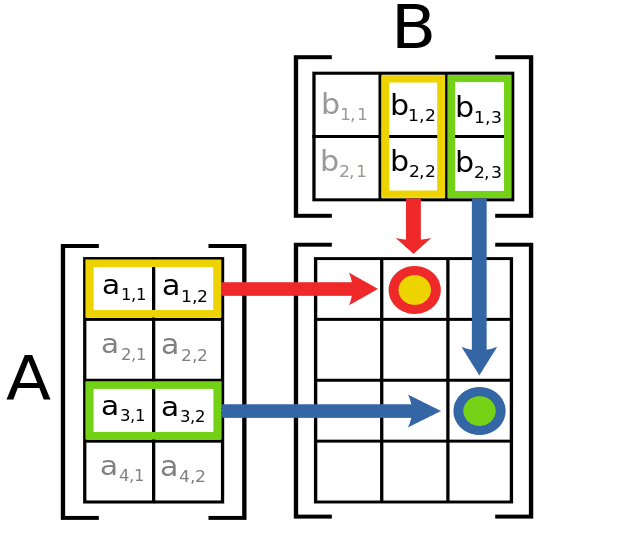
Previous Page Print Page. Let the resultant matrix upon multiplication of A and B be X with elements denoted by xij as shown. Direct Matrix multiplication of Given a matrix a matrix and a matrix then can be computed in two ways and.
We need to find the minimum value for all the k values where i. You said that computing a cell in C like c11 takes n2 is not really correct. Output Minimum number of matrix multiplication.
Calculating each cell alone like c11 takes n operations. So overall we use 3 nested for loop. Complexity of Direct Matrix multiplication.
Since then we have come a long way to better and clever matrix multiplication algorithms. Simply put your matrix C has n x n cells which requires n2 operations for all cells. Although it does not affect the product the order in which the terms are parenthesized affects the number of simple arithmetic operations needed to compute the product that is the computational complexity.
Begin define table minMul of size n x n initially. T n c i f n 1 7 x T n 2 d x n 2 o t h e r w i s e where c and d are constants. Matrix Multiplication operation is associative in nature rather commutative.
ONNN where N is the number present in the chain of the matrices. Let the input 4 matrices be A B C and D. Please refer to the following post as a prerequisite of the code.
So that would take O n3 time complexity in total. Solving the procedure manually would require nine separate calculations to obtain each element of the final matrix X. As we know that we use a matrix of NN order to find the minimum operations.

Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

Intro To Matrix Multiplication Video Khan Academy

2 9 Strassens Matrix Multiplication Youtube
Can You Multiply A 3x3 Matrix By A 2x3 Quora

Sparse Matrix Multiplication Description By Glyn Liu Medium

Matrix Multiplication In C Javatpoint

Python Matrix Multiplication Python Program To Perform Matrix Multiplication
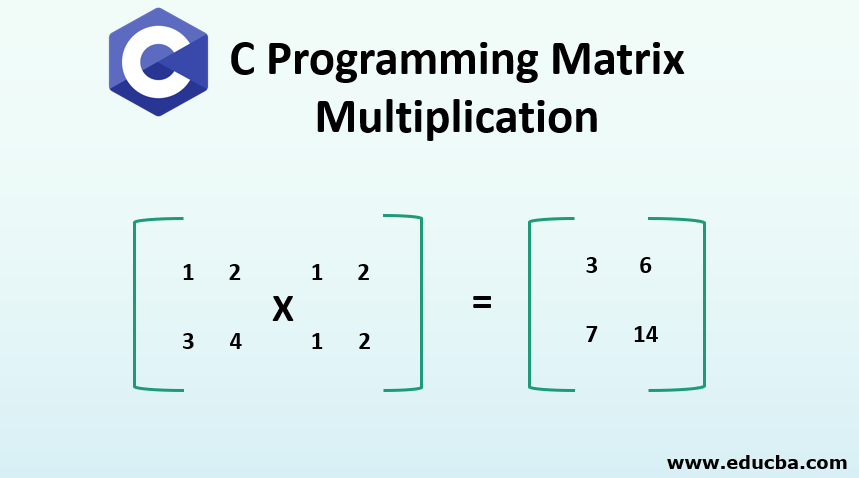
C Programming Matrix Multiplication C Program For Matrix Manipulation

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
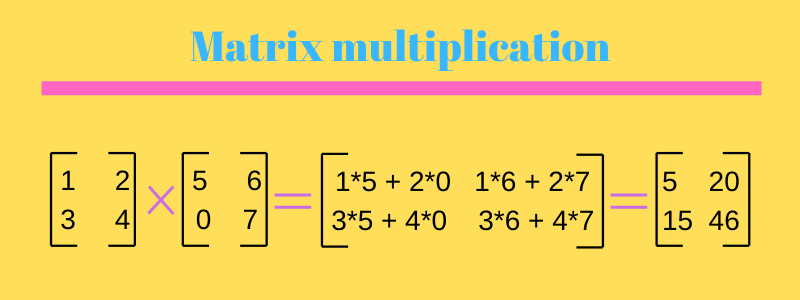
Matrix Multiplication In C Programming Simplified

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Performing Convolution By Matrix Multiplication F Is Set To 3 In This Download Scientific Diagram
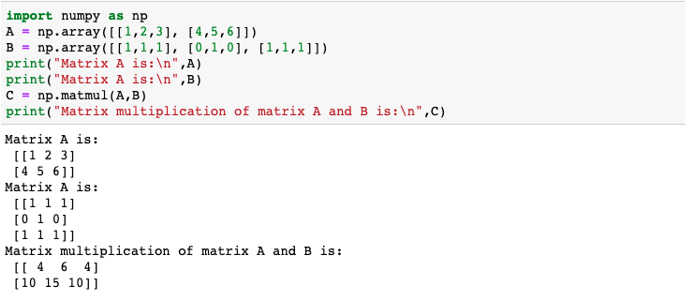
Matrix Multiplication In Numpy Different Types Of Matrix Multiplication
Matrix Multiplication Dimensions Article Khan Academy

Matrix Multiplication In Numpy Different Types Of Matrix Multiplication
Matrix Multiplication Concepts Methods Properties Videos And Examples
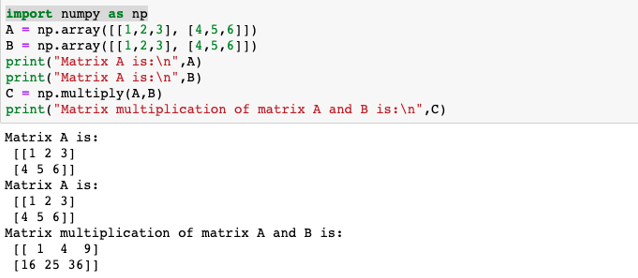
Matrix Multiplication In Numpy Different Types Of Matrix Multiplication
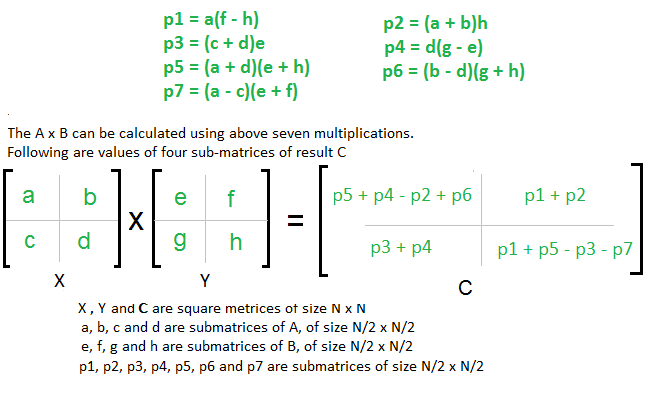
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks