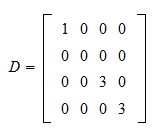Multiplying A Vector By A Diagonal Matrix
Ind ind 1. Multiplying a circulant matrix by a vector.

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download
Let E i be the n n matrix with a 1 on position i i and zeros everywhere else.

Multiplying a vector by a diagonal matrix. D diag v returns a square diagonal matrix with the elements of vector v on the main diagonal. Let A aik be an mn matrix and B bkj be an np matrix. A 1 n a 21 a 22.
The diagonal numbers change in each time step but for simplicity sake lets keep them all at 1 for the moment. When multiplying a lower triangular matrix L1 with ones on the main diagonal by a diagonal matrix D column n of the matrix product requires N n multiplications and no summations. Result_antidiagi this-diagonali mantidiagi this-antidiagi mdiagonalmsize-i-1.
Find A y where y 2 1 3 and A 1 2 3 4 5 6 7 8 9. Im not sure whether it answers your question but here is a matrix procedure to transform the column vector v into a diagonal matrix D. It is also called the scaling matrix because multiplication with the diagonal matrix scales an object in a corresponding vector space.
1 2 3 2 1 3 1 2 2 1 3 3 13. D diag vk places the elements of vector v on the k th diagonal. End end toc disptensorized version tic dd sumreshapexdd.
For int i 0. Vector t multiplied by diag matrix t vector t1 vector t1 multiplied by diag matrix t1 vector t2 vector t2 multiplied by diag matrix t2 vector t3. I then discussed block diagonal matrices ie block matrices in which the off-diagonal submatrices are zero and in a multipart series of posts showed that we can uniquely and maximally partition any square matrix into block.
A 2 n a m 1 a m 2. Proposition Let be a matrix and a diagonal matrix. On order to do so you need first to build a matrix out of the vector x.
What is the effect of pre-multiplying a matrix by a diagonal matrix A. A m n x 1 x 2 x n a 11 x 1 a 12 x 2 a 1 n x n a 21 x 1 a 22 x 2 a 2 n x n a m 1 x 1 a m 2 x 2 a m n x n. That is matrices are multiplied row by column.
The product AB is defined to be the mp matrix C cij such that cij Pn k1 aikbkj for all indices ij. Dispdense matrix multiply tic aa Dx. Now apply the hadamard multiplication to this tempMatrix with the identity matrix.
Similarly let e i be the 1 n row matrix with a 1 on position. A x a 11 a 12. The general formula for a matrix-vector product is.
Finally consider multiplying two diagonal matrices. An example of a diagonal matrix The following matrices may be confused as diagonal matrices. Let ymathsfDFTvecx F_n vecx denote the DFT of a vector vecx and let vecxmathsfDFT-1yF_n-1 vecy denote the inverse DFT.
I result_diagonali this-diagonali mdiagonali this-antidiagi mantidiagmsize-i-1. The successive rows of the original matrix are simply multiplied by successive diagonal elements of the diagonal matrix. Onesmatrixquestionm d 100.
XMatrix operatorconst XMatrix. Toc dispsparse matrix multiply tic bb Dsparsex. In this case all the off diagonal elements are assigned zero.
By the definition number of columns in A equals the number of rows in y. If C_n is circulant with vector representation veca_n then multiplying it by a size-n vector vecx can be written as. Diagonal matrices as was explained earlier are square matrices.
A diagonal matrix is a square matrix in which all entries are zero except for those on the leading diagonal. With n 1 N we get 1. X 11111 tempMatrix.
A y 1 2 3 4 5 6 7 8 9 2 1 3 First multiply Row 1 of the matrix by Column 1 of the vector. Multiplying two or more diagonal matrices produces a diagonal matrix. K0 represents the main diagonal k0 is above the main diagonal and kdiagonal.
For kk1d for jj1d cckk cckk xind. The effect is that of multiplying the i-th row of matrix A by the factor k i ie. Then the product is a matrix whose -th row is equal to the -th row of multiplied by for every.
All you have to compute are the diagonal elements. Effect of multiplying a matrix by a diagonal matrix. To find the value of each of the diagonal.
Matrix multiplication The product of matrices A and B is defined if the number of columns in A matches the number of rows in B. That is use the outer product with another vector which contains only 1 entries. In a previous post I discussed the general problem of multiplying block matrices ie matrices partitioned into multiple submatrices.
Toc dispfor loop version tic cc zerosd1. Multiplication by a diagonal matrix Two useful results about products involving diagonal matrices are reported below. It does basically element-wise multiplication of all elements.

How To Calculate The Inverse Of A Diagonal Matrix Quora
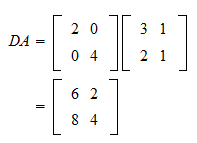
Multiplication By A Diagonal Matrix

How Do I Convert A N 1 Matrix To A N N Diagonal Matrix Stack Overflow

Product Of Two Diagonal Matrices Is Diagonal Youtube
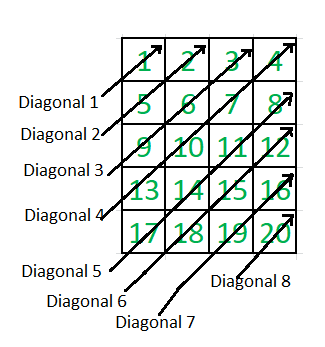
Zigzag Or Diagonal Traversal Of Matrix Geeksforgeeks

1 7 Diagonal Triangular And Symmetric Matrices Diagonal

Diagonal Matrix An Overview Sciencedirect Topics
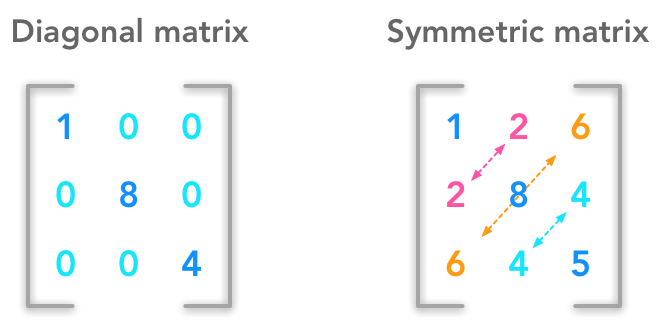
Introduction To Diagonal And Symmetric Matrices Unit And Orthogonal Vectors Using Python Numpy Examples And Drawings

Basis For The Definition Of A Diagonal Matrix Mathematics Stack Exchange

Block Diagonal Matrices Youtube
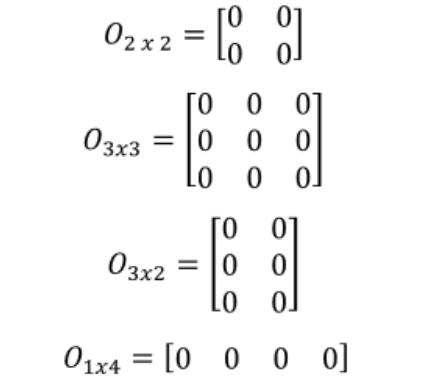
Definition Of A Zero Matrix Studypug
Is A Diagonal Matrix With All Diagonal Entries As 1 An Identity Matrix Quora

1 7 Diagonal Triangular And Symmetric Matrices Diagonal

Diagonal Matrix Definition Examples And Its Properties

Matrices Matrices A Matrix Is A Rectangular Array