Multiply Quaternion Matrices
It is given by the group presentation where e is the identity element and e commutes with the other elements of the group. In this video we will see that the quaternions may.
Cs184 Using Quaternions To Represent Rotation
Quaternion addition is simply the four-tuple addition of quaternion representations s 1 v 1 s 2 v 2 s 1 s 2 v 1 v 2.
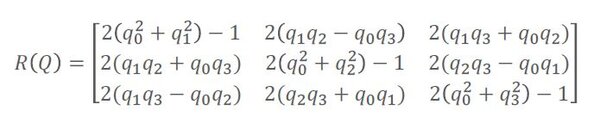
Multiply quaternion matrices. Now suppose I construct a quaternion matrix as described here. The quaternions as matrices To model the multiplication of quaternions form matrices as before but with the entries now being complex numbers rather than real numbers and with the bottom row being complex-conjugated. In Quaternion maths multiplying by the inverse is the equivalent of subtracting the rotation.
I also know that I can do quaternion multiplication to get the combined rotation of 2 quaternions q1 and q2 by using quaternion multiplication q q1q2 as expressed here. V v 2 r x s v r x v m. This example shows how to determine the product of 1-by-4 with two 1-by-4 quaternions.
Mult quatmultiply q r mult. The following two kinds of matrixs are very usefull for dynamic simulation. The set of all 3x3 matrices or all 4x4 matrices with standard matrix addition and multiplication is a ring but not a division ring because not all matrices have inverses.
Hence the use of terms like premultiplication and postmultiplication. In group theory the quaternion group Q 8 sometimes just denoted by Q is a non-abelian group of order eight isomorphic to the eight-element subset of the quaternions under multiplication. Doing that you will get a formula equivalent to the Euler-Rodrigues Formula 1.
Heres the code I use the multiply all 3 together-. QuaternionZ new Quaternion new Vector3f 0 0 1 rotationgetZ. RotationMatrix rotmat quat frame rotationMatrix 33 07071 -00000 -07071 03536 08660 03536 06124 -05000 06124.
To verify the rotation matrix directly create two rotation matrices corresponding to the rotations about the y - and x -axes. Then we have pq p0 q0 p1 q1ip2 q2j p3 q3k. More specifically consider the quaternion q above and another quaternion p p0 p1ip2j p3k.
This page discusses the equivalence of quaternion multiplication and orthogonal matrix multiplication. The inverse of a quaternion refers to the multiplicative inverse or 1 q and can be computed by q-1 q qq for any non-zero quaternion. Determine the Product of Two Different Quaternions.
That is to say that if C A inverse B then C B A. Multiply the rotation matrices and compare to. Every quaternion q has a negative q with components q i i.
Convert the quaternion to a rotation matrix. Quaternion matrix new Quaternion 0 0 0 0. Matrix matrixmultiply quaternionX quaternionY.
The right quaternions rotation is applied first and then the left quaternions. If a quaternion is represented by qw i qx j qy k qz then the equivalent matrix to represent the same rotation is. QuaternionX new Quaternion new Vector3f 1 0 0 rotationgetX.
Like with matrices the operation is carried out from right to left. Both matrix multiplication and quaternion multiplication are non-commutative. Another presentation of Q 8 is.
I know that for some rotation quaternion q w x y z I can find the rotation of point p1 by p2 qp1conjugate q. Notice that quaternion multiplication is associative q 1 q 2q 3 q 1 q 2 q 3 but is not commutative q 1 q 2 q 2 q 1. In math its usually possible to view an object or concept from many different but equivalent angles.
QuaternionY new Quaternion new Vector3f 0 1 0 rotationgetY. Q 1 0 1 0. Where x represents the cross product s and r are the scalar and vector parts of the quaternion respectively and m is the sum of the squares of the components of the quaternion.
Equations Quaternion multiplication and orthogonal matrix multiplication can both be used to represent rotation. Q QuaternionMultiplyqX qY. 2 1 01 01.
R 1 05 05 075. C m MatrixMultiplymX mY. Quaternion Multiplication We can perform multiplication on quaternions if we expand them into their complex number form If q represents a rotation and q represents a rotation then qq represents q rotated by q This follows very similar rules as matrix multiplication in particular it is not commutative qsiq 1 jq 2 kq 3 qqsiq 1 jq 2.
Multiplying quaternions Two quaternions can be concatenated by multiplying them together. Quaternion multiplication is defined as Equation 224. Transformations are concatenated in the same order for the QuaternionMultiply and MatrixMultiply methods.
21 Addition and Multiplication Addition of two quaternions acts componentwise. After encountering the concept of quaternion matrices I am a bit puzzled as to how one may multiply two of these things since there are. In the following C code example assuming that mX and mY represent the same rotations as qX and qY both m and q represent the same rotations.
E Ring Of Quaternions A Quaternion In Matrix Form Chegg Com
Cs184 Using Quaternions To Represent Rotation
Cs184 Using Quaternions To Represent Rotation
Orientation Quaternions Ppt Video Online Download
Add Quaternion Matrices And Quaternion Rates Matrices Issue 113 Moble Quaternion Github
Add Quaternion Matrices And Quaternion Rates Matrices Issue 113 Moble Quaternion Github
Quaternions As 4x4 Matrices Connections To Linear Algebra Youtube
Quaternion Vs Rotation Matrix 4 If We Write A Chegg Com
Process Of Creating First Order Quaternions From An Initial Rotation Download Scientific Diagram
Quaternions Topics Introduction To 3d Game Programming With Directx 12 Computer Science 2016
Unit Quaternion Description Of Spatial Rotation In 3d Electron Cryo Microscopy Biorxiv
4 If We Write A Quaternion As A 4 Vector Q A B C D Chegg Com
How To Convert A Quaternion To A Rotation Matrix Automatic Addison
