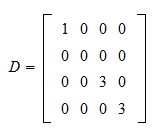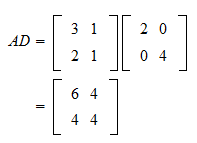Matrix Multiplication Only Diagonal
A square matrix A is called a diagonal matrix if all its nondiagonal entries are zeros. Z.
Diagonal Matrices 17 6 Sideway Output To
Therefore the product matrix is diagonal.

Matrix multiplication only diagonal. Toc dispsparse matrix multiply tic bb Dsparsex. Faten Said Abu-Shoga Islamic University of Gaza Chapter 2 21 Matrix Multiplication Lectures on Linear Algebra. Example The identity matrices and square zero matrices are diagonal matrices.
I then discussed block diagonal matrices ie block matrices in which the off-diagonal submatrices are zero and in a multipart series of posts showed that we can uniquely and maximally partition any square matrix into block. In a previous post I discussed the general problem of multiplying block matrices ie matrices partitioned into multiple submatrices. Its diagonal entries are where we have used the fact that if.
If all the diagonal entries of Λ are distinct it commutes only with diagonal matrices. Onesmatrixquestionm d 100. We want to multiply some matrix mathbfA with some diagonal matrix mathbfD.
Dispdense matrix multiply tic aa Dx. End end toc disptensorized version tic dd sumreshapexdd. Let A diags1s2sn B diagt1t2tn.
An n n matrix commutes with every other n n matrix if and only if it is a scalar matrix that is a matrix of the form where is the n n identity matrix and is a scalar. The effect is that of multiplying the i-th row of matrix A by the factor k i ie. Matrix multiplication The product of matrices A and B is defined if the number of columns in A matches the number of rows in B.
Cii aiibii and all other entries are 0. Instead of carrying out a bunch of multiplications by zero we replace the matrix multiplications by a for loop and elementwise multiplication. 7 0 0 0 1 0 0 0 2 denoted diag712.
A square matrix is called diagonal if all non-diagonal entries are zeros. Ind ind 1. For kk1d for jj1d cckk cckk xind.
The matrix can be partitioned into four 22 blocks. Let A aik be an mn matrix and B bkj be an np matrix. This fact together with the fact that the off-diagonal entries of are zero implies that the off-diagonal entries of are zero.
By the results in the previous section computing the product is the same as multiplying the rows of by the diagonal entries of. The successive rows of the original matrix are simply multiplied by successive diagonal elements of the diagonal matrix. That is matrices are multiplied row by column.
The product AB is defined to be the mp matrix C cij such that cij Pn k1 aikbkj for all indices ij. It is possible to use a block partitioned matrix product that involves only algebra on submatrices of the factors. In other words the center of the group of n n matrices under multiplication is the subgroup of scalar matrices.
What is the effect of post-multiplying a matrix by a diagonal matrix A. The partitioned matrix can then be written as. In contrast for each k consecutive equal diagonal entries in Λ we may allow A to have anything at all in the corresponding k by k square block with both corners on the main diagonal.
By a diagonal matrix A. As Z is huge I want to avoid the full out multiplication. Further C can be computed more efficiently than naively doing a full matrix multiplication.
If A and B are diagonal then C AB is diagonal. Then AB diags1 t1s2 t2sn tn rA diagrs1rs2rsn. Toc dispfor loop version tic cc zerosd1.
The diagonal entries form the diagonal of A. If A aij is a square matrix then the entries aii are called diagonal entries. Compute only diagonals of matrix multiplication in R.

The Identity Matrix And Its Properties Mathbootcamps
Is A Diagonal Matrix With All Diagonal Entries As 1 An Identity Matrix Quora
Introduction To Diagonal And Symmetric Matrices Unit And Orthogonal Vectors Using Python Numpy Examples And Drawings

Diagonal Matrix Definition Examples And Its Properties
Is A Diagonal Matrix With All Diagonal Entries As 1 An Identity Matrix Quora

1 7 Diagonal Triangular And Symmetric Matrices Diagonal

2 1 Operations With Matrices 2 2 Properties Of Matrix Operations Ppt Video Online Download

Matrices Matrix Multiplication Warm Up Subtract Don T Forget To Kcc Ppt Download

7 1 Matrices Vectors Addition And Scalar Multiplication

Product Of Two Diagonal Matrices Is Diagonal Youtube

Time Complexity Of Matrix Multiplication In Big Align Computer Science Stack Exchange

Basis For The Definition Of A Diagonal Matrix Mathematics Stack Exchange
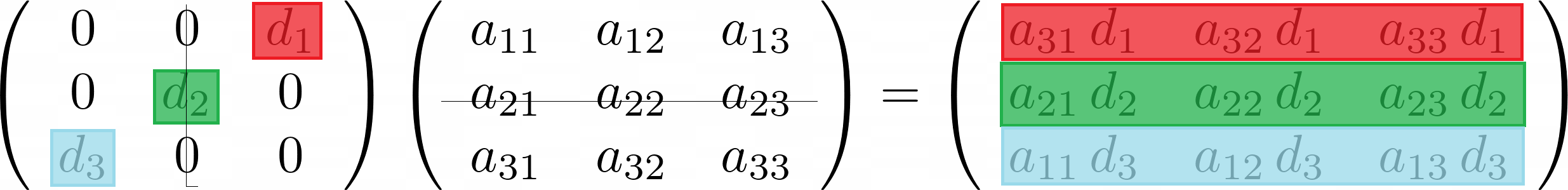
Visualizing Matrix Multiplication In Four Different Ways Part 2 By Vaibhav Patel Analytics Vidhya Medium