Matrix Matrix Multiplication Blocking
When implementing the above we can expand the inner most block matrix multiplication Aii kk Bkk jj and write it in terms of element multiplications. K bs block_mul Q.
Matrix Multiplication In Cuda A Simple Guide By Charitha Saumya Analytics Vidhya Medium
However it is also useful in computing products of matrices in a computer with limited memory capacity.
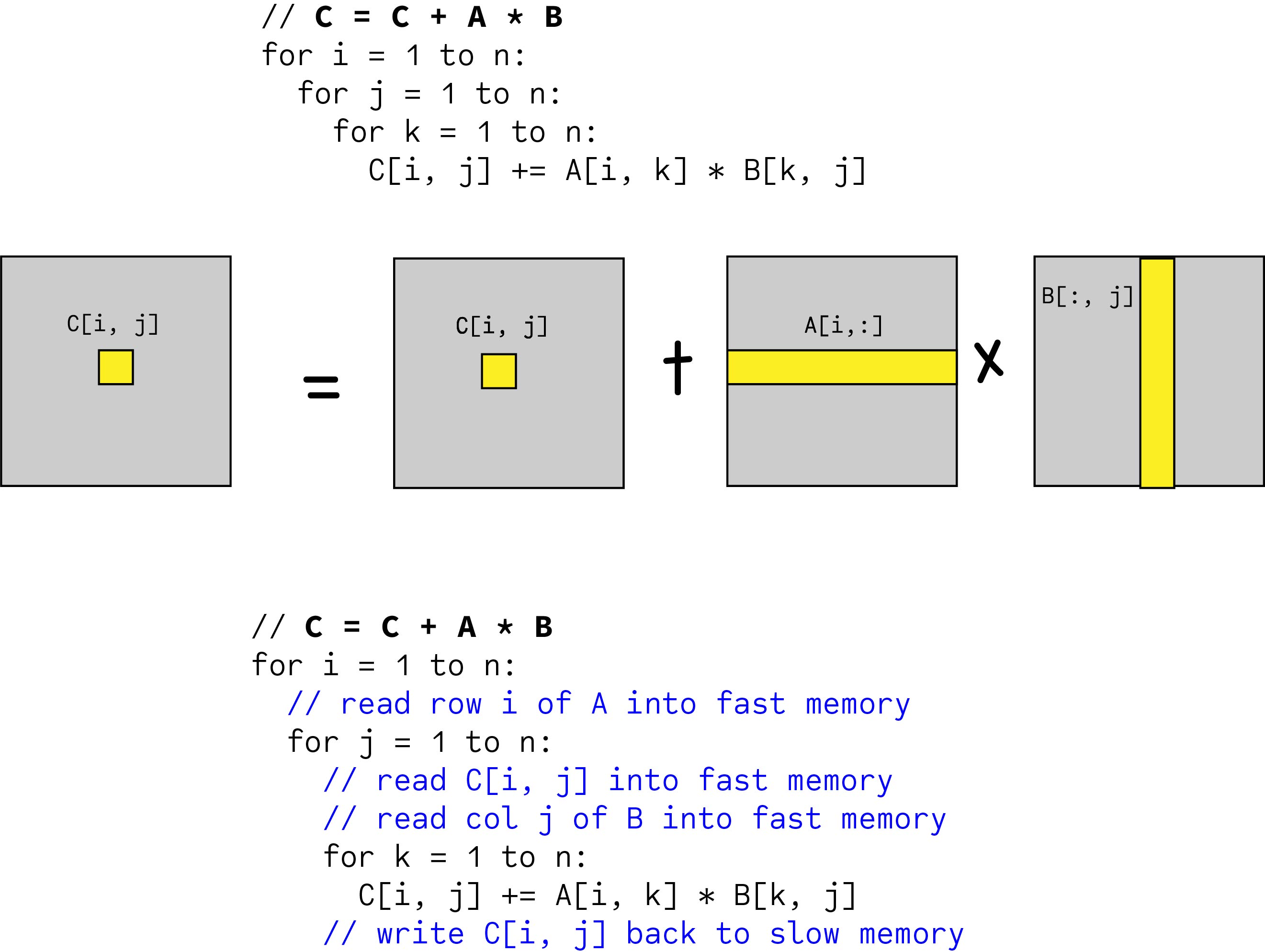
Matrix matrix multiplication blocking. What do we do with fringe blocks. The major difference from an unblocked matrix multiplication is that we can no longer hold a whole row of A in fast memory because of blocking. Typically an algorithm that refers to individual elements is replaced by one that operates on subarrays of data which are called blocks in the matrix computing field.
Let M m n denote any matrix of m rows and n columns irrespective of contents. 2 N3 nN nN read each block of A and B N3 times 2 N2 nN nN read and write each block of C once in the second nested loop N2 times. Then split A however.
Example of Block Compressed Sparse Row BCSR matrix format To access block rows data we need to get a number of blocks before the block row row_ptr block_row and multiply this value. While loop unrolling safe for most matrix sizes blocking is appropriate only for large matrices eg dont block for cache for 4x4 or 16x16 matrices. As such we are constantly accessing new values from memory and obtain very little reuse of cached data.
The matrices are partitioned into blocks in such a way that each product of blocks can be handled. In particular exible thinking about the process of matrix multiplication can reveal concise proofs of important theorems and expose new results. I want to perform a block matrix multiplication Divide a matirix into multiple sxs matrices and multiply the corresponding blocks.
For I 0. If the matrices are smaller the blocked code can be slower The result is a gap between performance realized by compiled code and the achievable performance Performance Gap in Compiled. To achieve the necessary reuse of data in local memory researchers have developed many new methods for computation involving matrices and other data arrays 6 7 16.
Load block CIJ into fast memory for k 1N load blocks AIK and BKJ into fast memory K k-1N1kN. For int jj0jj. CIJ CIJ AIKBKJ.
Block multiplication has theoretical uses as we shall see. We know that M m n M n q works and yields a matrix M m q. Algebra is best done with block matrices.
J bs block_clear. For int k kk. Rearrange for smaller working set.
The improvement n3Nn2 nN b. BLOCK_MULTIPLYCij Aik Bkj b Number of memory accesses. J ns.
The matrix can be partitioned into four 22 blocks. Matrix Multiplication as an Example. End store block CIJ end end Following the previous analysis we nd there are 2N2 2N3 loads and stores of blocks with this algorithm.
Then blocked matrix-matrix multiplication proceeds exactly as does a regular matrix-matrix multiplication except that individual multiplications of scalars commute while in general individual multiplications with matrix blocks submatrices do not. Viewing linear algebra from a block-matrix perspective gives an instructor access. Blocked Matrix Multiplication.
The partitioned matrix can then be written as. Since each block has size b b this gives. Split A by columns into a block of size a and a block of size b and do the same with B by rows.
2 A Blocked Version of Matrix Multiply Blocking a matrix multiply routine works by partitioning the matrices into submatrices and then exploiting the mathematical fact that these submatrices can be manipulated just like scalars. Then we can partition each matrix. J temp 0.
I have written the code as following the sample code of architecture book of Hennesy. I bs for J 0. This transformation is called loop tiling.
Cache Blocking In the above code for matrix multiplication note that we are striding across the entire A and B matrices to compute a single value of C. It is possible to use a block partitioned matrix product that involves only algebra on submatrices of the factors. Next we will analyze the memory accesses as we did before.
For K 0. Then the blocks are stored in auxiliary memory and their products are computed one by one. Better locality through blocking Basic idea.
For example suppose we want to compute C AB where A B and C are each 88 matrices. Listen to my latest Novel narrated by me.
Matrix Matrix Multiplication Ml Wiki
Parallel Matrix Multiplication C Parallel Processing By Roshan Alwis Tech Vision Medium
Performance X64 Cache Blocking Matrix Blocking Youtube
Matrix Matrix Multiplication Ml Wiki
Blocked Matrix Multiplication Malith Jayaweera
Matrices Matrix Multiplication Examsolutions Youtube
Understanding Matrix Multiplication On A Weight Stationary Systolic Architecture Telesens
Blocked Matrix Multiplication Malith Jayaweera
Blocked Matrix Multiplication Malith Jayaweera
Blocked Matrix Multiplication Malith Jayaweera
Blocked Matrix Multiplication Malith Jayaweera
5 2 1 Partitioned Matrix Matrix Multiplication Youtube
Blocked Matrix Multiplication Malith Jayaweera
Multiplication Of Matrix Using Threads Geeksforgeeks
Codebox Create Image Filters With Matrix Multiplication Make
Matrix Multiplication Is A Key Computation Within Many Scientific Applications Particularly Those In Deep Learning Many Operations In Modern Deep Neural Netwo
