Matrix Inner Product Space
A b in mathbbC 2 A vector space with an inner product consisting of all vectors of the form V afrangle bg rangle. The inner product ab of a vector can be multiplied only if a vector and b vector have the same dimension.

Vector Spaces And Inner Product Spaces
For any vectors u v w and a real number r R.
Matrix inner product space. Then B PTAP. Inner product bf acdot bf bc scalar. The matrix inner product is the same as our original inner product.
Here Rm nis the space of real m nmatrices. The following properties of inner product are immediate consequences of the def-inition. Positive-definiteness Ifx6 0 thenhx xi Randhx xi0.
When Fnis referred to as an inner product space you should assume that the inner product is the Euclidean inner product unless explicitly told otherwise. The standard inner product between matrices is hXYi TrXTY X i X j X ijY ij where XY 2Rm n. Equivalently fl flhuvi fl.
IfFRVis areal innerproduct space. In mathematics the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers usually coordinate vectors and returns a single numberIn Euclidean geometry the dot product of the Cartesian coordinates of two vectors is widely used. 5 Cauchy-Schwarz inequality Theorem 51 Cauchy-Schwarz Inequality.
Since your inner product is symmetric so is the matrix B. It is often called the inner product or rarely projection product of Euclidean space even though it is not. An inner product space is a vector space Valong with an inner product on V.
A b in mathbbC Where frangle g rangle represent sin x cos x. In mathematics the tensor product of two vector spaces V and W over the same field is a vector space which can be thought of as the space of all tensors that can be built from vectors from its constituent spaces using an additional operation which can be considered as a generalization and abstraction of the outer productBecause of the connection with tensors which are the elements of a. The Euclidean inner product of two vectors x and y in ℝ n is a real number obtained by multiplying corresponding components of x and y and then summing the resulting products.
If P is the transition matrix from B to B0. This says that the columns of B express the images phie_j in the chosen dual basis ofV so B is the matrix of phi with respect to the chosen bases of V and of V. Let AB be matrices of the inner product relative to bases BB0 of V respectively.
The outer product a b of a vector can be multiplied only when a vector and b vector have three dimensions. IfFCV is acomplex inner product space. A vector space with an inner product is aninner product space.
Inner Product on a Real Vector Space Let V be a real vector space. For any vectors uv in an inner product space V huvi2 huuihvvi. Let V be a flnite-dimensional inner product space.
A vector space with an inner product defined on it is called an inner product space. You could write this asV asin x bcos x. If X is a real vector space then property I2 reduces to hxyi hyxi.
1 A function space with an inner product consisting of all linear combinations of cos x and sin x. Then you may as well write phie_jsum_i1nb_ijei instead of what is in the question. The inner product of a vector with itself is positive unless the vector is the zero vector in which case the inner product is zero.
Cross product bf atimes bf bbf c vector. The most important example of an inner product space is Fnwith the Euclidean inner product given by part a of the last example. TrZ is the trace of a real square matrix Z ie TrZ P i Z ii.
An inner product on V is a function that assigns a real number u v to each pair of vectors u and v in V satisfying the following properties. A hx0i h0xi for all x X b hax byzi ahxyi bhxzi for all xyz X and ab F Example 75 and.

Chap 5 Inner Product Spaces 5 1 Length And Dot Product In R N 5 2 Inner Product Spaces 5 3 Orthonormal Bases Gram Schmidt Process 5 4 Mathematical Models Ppt Download

When A Moves From One Side Of The Dot Product To The Other It Becomes A T Mathematics Stack Exchange
Inner Dot Product Of Two Vectors Applications In Machine Learning

Chapter 7 Inner Product Spaces Ppt Download

For Any Inner Product Can We Always Find A Symmetric Orthonormal Basis Mathematics Stack Exchange

Lecture 11 Inner Product Space Ppt Download

If The Inner Product Of Two Matrices Is Zero What Does That Mean

If The Inner Product Of Two Matrices Is Zero What Does That Mean

Chapter 7 Inner Product Spaces Ppt Download
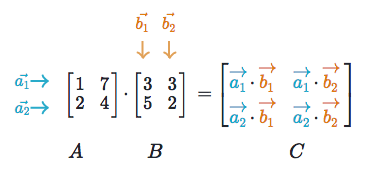
Linear Algebra Ml Glossary Documentation

What Is Wrong With My Proof That X Hy X Ty For Any Complex Vectors X Y Mathematics Stack Exchange

For Any Inner Product Can We Always Find A Symmetric Orthonormal Basis Mathematics Stack Exchange
Inner Dot Product Of Two Vectors Applications In Machine Learning

Elementary Linear Algebra Anton Rorres 9th Edition Ppt Download
Inner Dot Product Of Two Vectors Applications In Machine Learning

Linear Algebra Inner Product Space Gram Schmidt Orthogonal Complement Mat223 Past Test Youtube

The Difference Between The Dot Product And The Inner Product Youtube

Chapter 7 Inner Product Spaces Ppt Download

Dot Product Vs Inner Product Mathematics Stack Exchange