Matrix Chain Multiplication Algorithm In Daa
There are three cases by which we can solve this multiplication. I.

Matrix Chain Multiplication Dp 8 Tutorialspoint Dev
Array1n 1n others 0.

Matrix chain multiplication algorithm in daa. Three Matrices can be multiplied in two ways. For k 1 to columnsA 7. First multiplying A 2 and A 3 then multiplying and resultant withA 1.
Do m i i 0 4. N 4 arr 10 30 5 60 Output. Algorithm of Matrix Chain Multiplication MATRIX-CHAIN-ORDER p 1.
P 10 20 30 Output. Let we have n number of matrices A1 A2 A3 An and dimensions are d0 x d1 d1 x d2 d2 x d3. CostRec-Matrix-Chainp i k Rec-Matrix-Chainp k 1 j pi 1pkpj.
Let the input 4 matrices be A B C and D. 6000 There are only two matrices of dimensions 10x20 and 20x30. Do for j 1 to columnsB 5.
N-1 loop for i in 1. Do q m i k m k 1 j p i-1 p k p j 10. Do Cij 0 6.
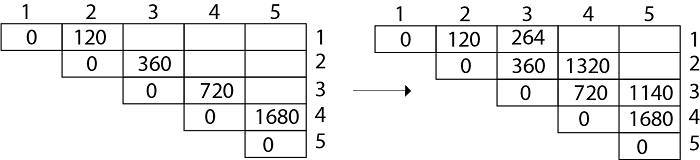
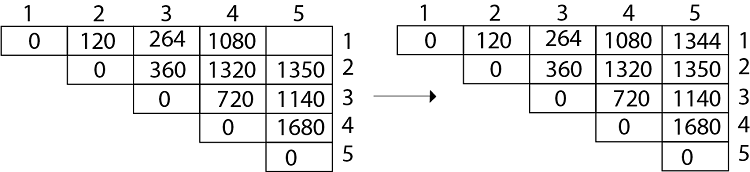
Do for i 1 to n-l 1 6. In the example of Figure 161 the call MATRIX-CHAIN-MULTIPLYA s 1 6 computes the matrix-chain product according to the parenthesization A 1 A 2 A 3A 4 A 5A 6. Len Subsequence lengths for i 1.
Matrix Chain Multiplication Using Dynamic Programming. J-1 loop current Mi k Mk1 j di-1dkdj if current min then min current end if. For len 2.
For l 2 to n l is the chain length 5. N - diagonal loop j i diagonal. Mij Minimum number of scalar multiplications ie cost needed to compute the matrix AiAi1Aj Aij The cost is zero when multiplying one matrix for i 1.
M 3 5 1140. The important point is that when we use the equation to calculate we must have already evaluated and For both cases the corresponding length of the matrix-chain are both less than. The matrices have dimensions 1030 305 560.
Mij 8. As Comparing both output 1140 is minimum in both cases so we insert 1140 in table and M 3 x M 4 M 5 this combination is chosen for the output making. Out of all possible combinations the most efficient way is A BCD.
M 1 4 M 1 M 2 M 3 M 4. Matrix Chain Multiplication Consider the case multiplying these 4 matrices. If cost.
For k in i. 2 then X MATRIX-CHAIN-MULTIPLYA s i si j 3 Y MATRIX-CHAIN-MULTIPLYA s si j 1 j 4 return MATRIX-MULTIPLYX Y 5 else return A i. A j A i A i1 A i2 A i3.
To illustrate the different costs incurred by different paranthesization of a matrix product. Say the matrices are named as A B C D. Solving a chain of matrix that A i A i1 A i2 A i3.
For k i to j-1 9. The minimum number of multiplications are obtained by putting parenthesis in following way ABCD -- 102030 103040 104030 Input. Matrix-MultiplyAB 1If columnsArowsB 2.
Using Naïve method two matrices X and Y can be multiplied if the order of these matrices are p q and q r. For i 1 to n 3. D n-1 x d n ie Dimension of Matrix A i is d i-1 x d i.
Compute the value of an optimal solution in a bottom-up fashion. Developing a Dynamic Programming Algorithm Step 3. The time to compute C is dominated by the number of scalar multiplications.
Only defined for. Matrix Chain Multiplication using Dynamic Programming FormulaPATREON. The number of operations are - 203010 402010 401030 26000.
Else for i 1 to rowsA 4. Following is the algorithm. Then error incomplete dimensions 3.
Now Product of 4 matrices. Here we are calculating Z X Y. The Design and Analysis of Algorithms pdf notes DAA pdf notes book starts with the topics covering AlgorithmPsuedo code for expressing algorithms Disjoint Sets- disjoint set operations applications-Binary search applications-Job sequencing with dead lines applications-Matrix chain multiplication applications-n-queen problem.
Matrix-Multiplication X Y Z for i 1 to p do for j 1 to r do Z ij 0 for k 1 to q do Z ij Z ij X ik Y kj. Dynamic Programming Data Structure Algorithms If a chain of matrices is given we have to find the minimum number of the correct sequence of matrices to multiply. M 1 x M 2 x M 3 M 4.
Return final cost This version which is based directly on the recurrence the recursive formulation that we gave for chain matrix problem seems much simpler. I m i i 0. Update if better return mij.
ABCD - This is a 2x2 multiplied by a 2x1. Matrix Ai has dimension dimsi-1 x dimsi for i 1n MatrixChainOrder int dims lengthdims n 1 n dims. Do j i l -1 7.
ABCD - This is a 2x4 multiplied by a 4x1 so 2x4x1 8 multiplications plus whatever work it will take to multiply BCD. So what is wrong with this. First multiplying A 1 and A 2 then multiplying and resultant withA 3.
For diagonal in 1. No of Scalar multiplication in Case 1 will be. We know that the matrix multiplication is associative so four matrices ABCD we can multiply A BCD AB CD ABCD A BCD in these sequences.

Dynamic Programming 3 Example Matrix Chain Multiplication N N What If We Want To Multiply A String Of More Than Two Matrices Together Matrix Course Hero

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube
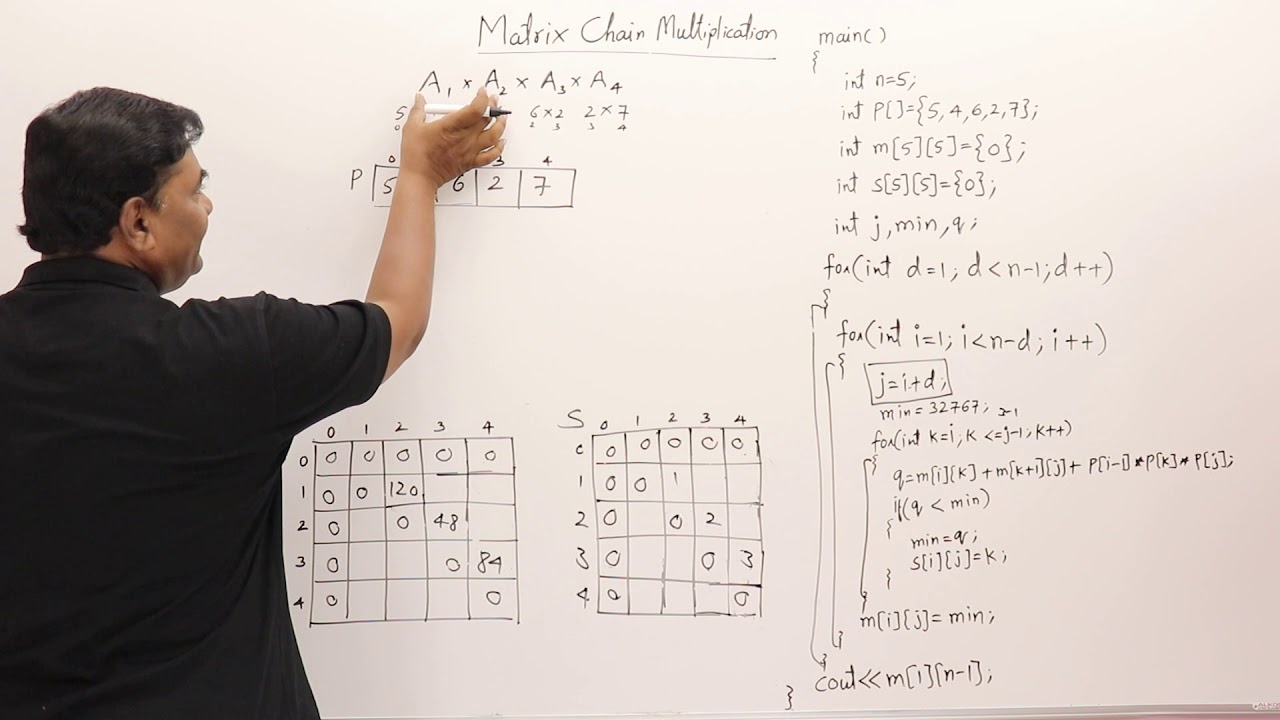
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube

Solved Consider The Matrix Chain Multiplication Problem T Chegg Com

Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium

Matrix Chain Multiplication Problem Using Dynamic Programming Part 1 Youtube

New Matrix Chain Multiplication Using Dynamic Programming Formula Youtube

Matrix Chain Multiplication Dynamic Programming Youtube
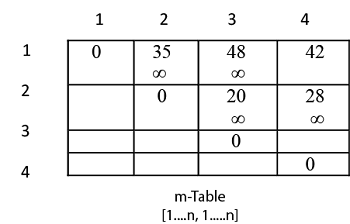
Matrix Chain Multiplication Algorithm Javatpoint

Unit 4 Dynamic Programming Ppt Video Online Download
Matrix Chain Multiplication Algorithm Javatpoint