Symmetric Matrix Times Antisymmetric Matrix
If A is an invertible symmetric matrix then A-1 is also symmetric. Some of the symmetric matrix properties are given below.
De nition 1 Let U be a d dmatrix.

Symmetric matrix times antisymmetric matrix. Real lambda orthogonal x. Product of Symmetric and Antisymmetric Matrix. The next result follows easily from Theorem 114.
Symmetric matrix of well-determined rank are designed so that the iterates converge to x and the iterations are terminated when a good approximation of x has been computed. This implies that UUT I by uniqueness of inverses. We solve a problem in linear algebra about symmetric matrices and the product of two matrices.
C C T 4 3 2 5 1 6 3 8 1 4 5 3 3 1 8 2 6 1 0 2 1 2 0 2 1 2 0 is skew-symmetric. Itexa_ijitex doesnt denote a matrix. Symmetric matrix is used in many applications because of its properties.
Then Pf M 1 n 12detA. If A and B are symmetric matrices then ABBA is a symmetric matrix thus symmetric matrices form a so-called Jordan algebra. If we multiply a symmetric matrix by a scalar the result will be a symmetric matrix.
The commutator of matrices of the same type both symmetric or both antisymmetric is an antisymmetric matrix. A peculiarity that square matrices have is that they can be decomposed into the sum of a symmetric matrix plus an antisymmetric matrix. S 2 1 1 2 and A 0 1 1 0.
The diagonal elements of a skew symmetric matrix are equal to zero. Every square matrix A can be decomposed uniquely as the sum of two matrices S and V where S is symmetric and V is skew-symmetric. Perhaps the most important and useful property of symmetric matrices is that their eigenvalues behave very nicely.
Where is a free parameter. Hi I want to show that the Trace of the Product of a symetric Matrix say A and an antisymetric B Matrix is zero. I times something on the imaginary axis.
See 10 11 15 and references therein. Since texbeginpmatrix1 0 0 1endpmatrixbeginpmatrix0 1 -1 0endpmatrixbeginpmatrix0 1 -1 0endpmatrixneq 0tex its not true that the product of a symmetric and an antisymmetric matrix is 0. Because the matrix A is singular there are in nite number of solutions.
The definition of symmetric matrices and a property is given. Ψ x 1 x 2 x 1 0 Pauli principle indistinguishability and statistics. In that case we dont have real eigenvalues.
A simple example of this phenomenon is the following. Also for the matrix for all the values of i and j. A matrix can be skew symmetric only if it is square.
The symmetric matrix should be a square matrix. Start date Apr 7 2015. We remark that often linear discrete ill-posed problems with a symmetric matrix arise as normal equations 15.
When P2 Id 㱺 eiɸ 1 Ψ antisymmetric under permuation antisymmetric. If the transpose of a matrix is equal to the negative of itself the matrix is said to be skew symmetric. 16 To prove eq.
16 we write Mdefined by eq. In fact we are sure to have pure imaginary eigenvalues. It denotes the component on row i column j of a matrix.
The eigenvalue of the symmetric matrix should be a real number. Let Abe a real symmetric matrix of size d dand let Idenote the d didentity matrix. 15 as 9 M O A AT O O 1 AT O O 1 1 O O A 1 O 17 where 1isthe nnidentity matrix.
The formula that allows us to do it is the following. Is known then the second product can be replaced by its transpose. The commutator of a symmetric matrix with an antisymmetric matrix is always a symmetric matrix.
So thats the symmetric matrix and thats what I just said. Any power A n of a symmetric matrix A n is any positive integer is a symmetric matrix. Feb 3 2015 471.
Special types of square matrix Diagonal matrices lower and upper traingular matrices symmetric and antisymmetric matrices orthogonal matri-ces AT A 1 Hermetian matrix A Ayor Ay A unitary matrix Ay A 1 essentially a generalization of. Where C is the square matrix that we want to decompose C T its transpose and finally S and A are the symmetric and antisymmetric matrices respectively into which matrix C is decomposed. The matrix U is called an orthogonal matrix if UTU I.
Furthermore once the matrix product. Also we could look at antisymmetric matrices. This means that for a matrix to be skew symmetric A-A.
If the matrix is invertible then the inverse matrix is a symmetric matrix. The matrix product does not preserve the symmetric nor the anti-symmetric property. Thread starter 1 ognik Active member.
Antisymmetric matrix written in block form M O A AT O 15 where Ais an n ncomplex matrix and O is the n nzero matrix. I am studying the Klein-Gordon equation that is invariant under Lorentz transformation the infinitesimal transformation gives us. Multiplication of symmetric and antisymmetric tensors times a vector a question about indices.
δxμ ϵμνxν δϕ 1 2ϵμνMμνϕ with ϵμν ϵνμ antisymmetric. The transpose is minus the matrix. Which is symmetric nor anti-symmetric.
Similarly Again this is not symmetric nor anti-symmetric.
What Is A Skew Symmetric Matrix Quora

Given Ax T B T X B A Is A Symmetric Matrix And B Is An Antisymmetric Matrix Mathematics Stack Exchange

Symmetric And Skew Symmetric Matrices Definition Theorem Solved Example Problems

Symmetric And Skew Symmetric Matrices Form A Subspace Un Symmetric Matrices Don T P 3 1 18 Youtube

Symmetric And Skew Symmetric Matrix Assignment Help Math Homework Help Online Math Tutors

Mathematics Symmetric Skew Symmetric And Orthogonal Matrix Youtube

Solved If A Is Skew Symmetric Show That For Real Vectors Chegg Com

7 1 Matrices Vectors Addition And Scalar Multiplication
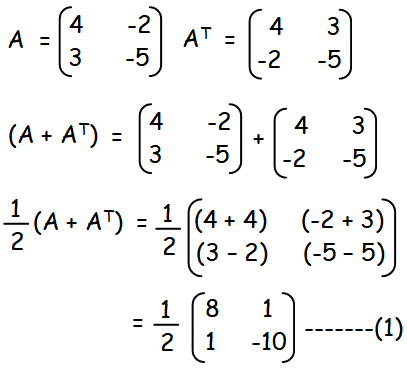
How To Express The Given Matrix As Sum Of Symmetric And Skew Symmetric
What Is A Skew Symmetric Matrix Quora

Skew Symmetric Matrices Lesson Robot Academy

Derivative Of A Rotation Matrix Robot Academy
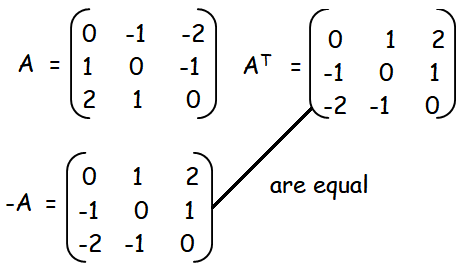
Questions On Symmetric And Skew Symmetric Matrix

Symmetric And Skew Symmetric Matrix Theorems Videos And Examples

Derivative Of A Rotation Matrix Robot Academy

Class 12 Symmetric And Skew Symmetric Matrices Youtube

Symmetric Skew Symmetric Matrices Definition With Examples


