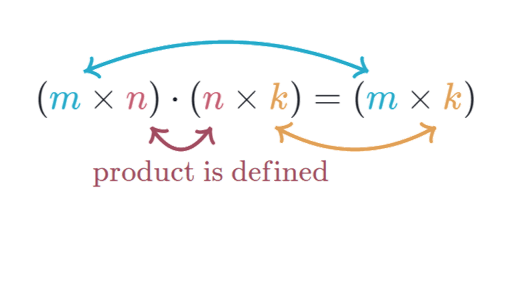Space Complexity For Matrix Multiplication
Naively we would need to multiply four such halves but in fact there is a way to do with only three. Space Complexity Matrix Chain Multiplication using Dynamic Programming Matrix Chain Multiplication Firstly we define the formula used to find the value of each cell.

Numerical Algorithms Matrix Multiplication Ppt Download
T On3 S Olog n Strassen algorithm.

Space complexity for matrix multiplication. The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input. The basic algorithm of matrix chain multiplication-. This is similar to matrix multiplication algorithms such as Strassens The algorithm described by the exercise is known as Karatsuba multiplication.
Up to 10 cash back Abstract. It will not be On2 in the general case. We consider the problem of multiplying sparse matrices over a semiring where the number of non-zero entries is larger than main memory.
P 10 20 30 40 30 Output. 30000 There are 4 matrices of. Worst case time complexity.
In the classical paper of Hong and Kung STOC 81 it was shown that to compute a product of dense U U matrices Theta left U3 B sqrt M right IOs are necessary and sufficient in the IO model with. Complexity of Direct Matrix multiplication. Yes all algorithms which stem from Strassens original algorithm this includes most known n 3 ε algorithms for matrix multiplication but not all -- see the comments have space complexity Θ n 2.
Any subcubic-time algorithm for matrix multiplication has superlogarithmic space complexity. M ij equals the minimum cost for computing the sub-products A ik and A k1j plus the cost of. In normal programming you will be allowed to use 256MB of space for a particular problem.
If you could find a n 3 ε time algorithm with p o l y log n space complexity this would be a great advance. And then multiplying this M P matrix by C requires multiplying and adding P terms for each of M N entries. Mi j min mi k mik j pi-1pkpj if i j.
So the total complexity is. Where p is dimension of matrix i k j. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions.
Combine these submatricies into our new matrix C. Following is simple Divide and Conquer method to multiply two square matrices. Ae bg af bh ce dg and cf dh.
2 Calculate following values recursively. Compute the submatricies of C. If all of those are n to you its On3 not On2.
Direct Matrix multiplication Given a matrix and a matrix the direct way of multiplying is to compute each for and. As before if we have n matrices to multiply it will take On time to generate each of the On 2 costs and entries in the best matrix for an overall complexity of On 3 time at a. For example 10100010 would be divided into 1010 and 0010.
1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram. Calculate the 7 matrix multiplications recursively. 2 same quadratic space complexity for all the other fast algorithms we studied.
So the complexity is O N M P. Note that has entries and each entry takes time to compute so the total procedure takes time. The standard way of multiplying an m-by-n matrix by an n-by-p matrix has complexity Omnp.
All the space required for the algorithm is collectively called the Space Complexity of the algorithm. The naive matrix multiplication for A B involves multiplying and adding N terms for each of M P entries in A B. 281 S On.
Θn28074 Best case time complexity. Let the input 4 matrices be A B C and D. So you cant create an array of size more 108 because you will be allowed to use only 256MB.

Matrix Multiplication Algorithm Wikiwand

Java Program To Multiply 2 Matrices Javatpoint

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm
Matrix Multiplication Dimensions Article Khan Academy

Numerical Algorithms Matrix Multiplication Ppt Download
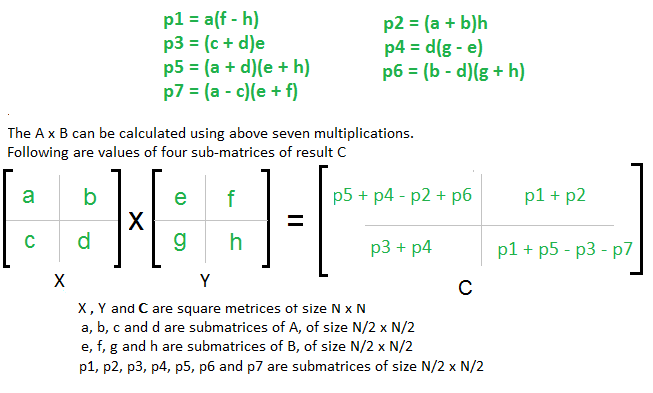
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks
Https Www Cs Colorado Edu Srirams Courses Csci3104 Spr15 Lectures L2note Pdf

2 9 Strassens Matrix Multiplication Youtube
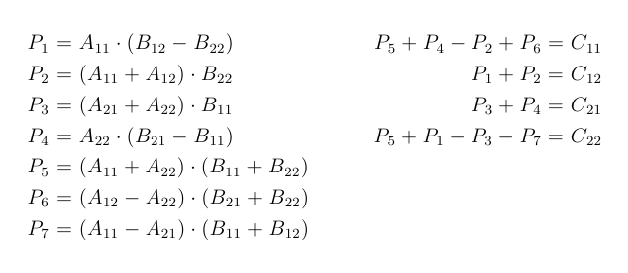
Strassen Matrix Multiplication C The Startup
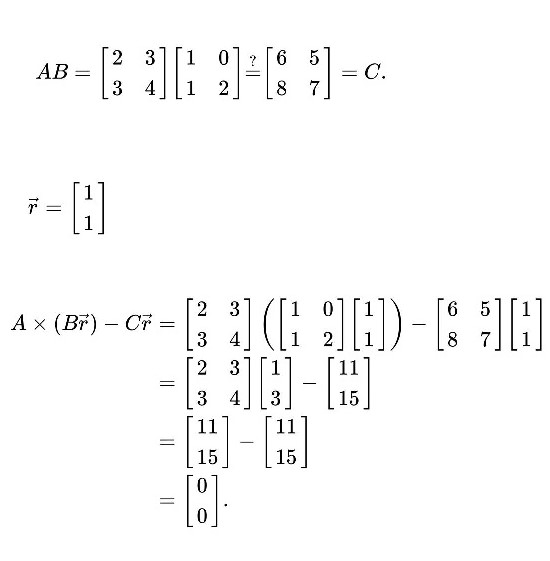
Freivalds Algorithm For Verifying Matrix Multiplication
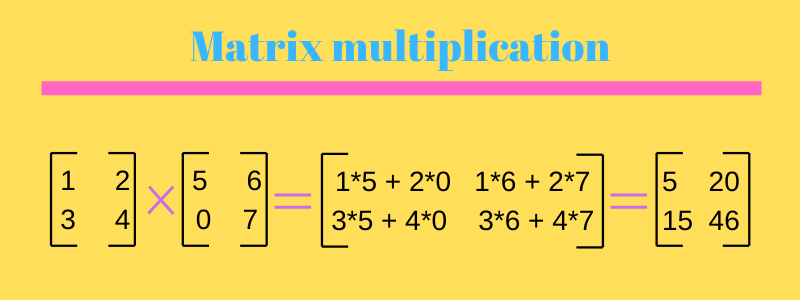
Matrix Multiplication In C Programming Simplified

Iterative Analysis Time Complexity Of Matrix Multiplication Data Structures Lecture Series Youtube

3 Complex Matrix Multiplications A 2 2 Matrix Multiplication B Download Scientific Diagram
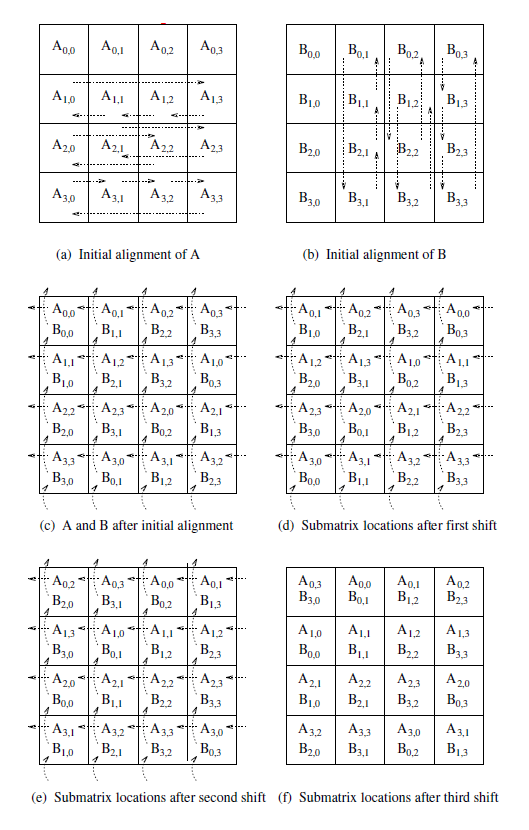
Cannon S Algorithm For Distributed Matrix Multiplication
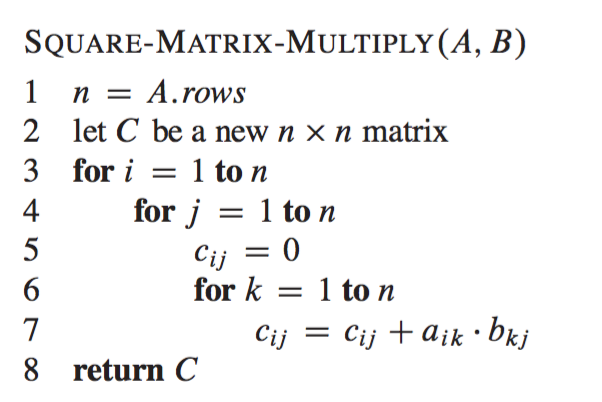
Matrix Multiplication Using The Divide And Conquer Paradigm

Matrix Multiplication Algorithm Wikiwand
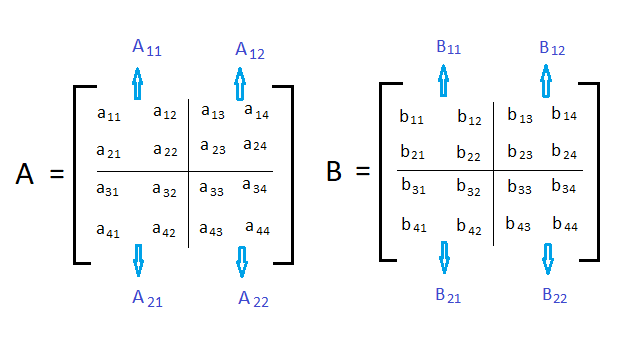
Strassen S Matrix Multiplication Algorithm Know Program