Matrix Multiplication Left To Right
Matrix multiplication is defined so that it works right to left just like function composition. Multiplication of two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix.
Multiplying Matrices Article Matrices Khan Academy
These matrices may be multiplied by each other to create a 2 x 3 matrix.
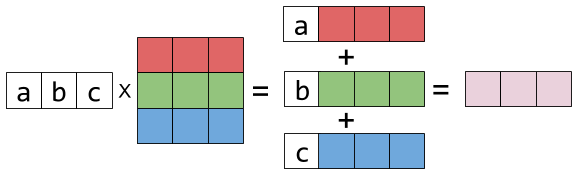
Matrix multiplication left to right. Ax x where A is a matrix and x the transformed point you just need to swap the second and third column. The result is another column vector - a linear combination of X s columns with a b c as the coefficients. Determine which one is the left and right matrices based on their location.
Since I havent decided which are the two bases to be used to represent those x F n L x F m how to even compute the multiplication A x. Sticking the white box with a in it to a vector just means. Its also why we conventionally represent vectors as column matrices.
D A B C. An easy way to determine this is to write out each matrixs rows x columns and if the numbers on the inside are the same they can be multiplied. We denote the columns of a matrix A by A j as follows 212 A A 1 A 2 A n Therefore A j is the j t h column of A when counted from left to right.
In order for matrix multiplication to work the number of columns of the left matrix MUST EQUAL to the number of rows of the right matrix. In mathematics if three matrices A B and C are multiplied such that a fourth matrix D A B C then the order must be computed right to left. Lets begin by looking at the right-multiplication of matrix X by a column vector.
Lets say we have three matrices a B and C and lets say that B and C are both M by n matrices and that a is a lets call it a K by M matrix and what I want to do is figure out whether matrix products exhibit the distributive property so lets test out a times B plus C a times B plus C and of course these are all matrices so B just to make things clear be the matrix B could be represented as. 2 x 3 times 3 x 3. Mathtt T cdot left beginarrayc mathbf x 1endarray right left beginarrayc smathtt Rcdot mathbf x mathbf t 1endarray right Note that rotation and scaling commutes.
If you multiply from the right eg. If you multiply from the left eg. It depends if you transform your points by multiplying the matrix from the left or from the right.
Multiply this vector by the scalar a. This allows matrices to represent linear transformations more intuitively. F n F m L A x A x for any x F n which is a left-multiplication transformation defined using a matrix A.
Smathtt Rcdot mathbf xmathtt Rscdot mathbf x. The individual elements of the matrix are called entries or components of A. Two matrices can only be multiplied if the number of columns of the matrix on the left is the same as the number of rows of the matrix on the right.
F x g y f f 1 x g f 1 y. Due to the matrix multiplication rules not all matrices can be multiplied. If A is an m -by- n matrix and B is an n -by- p matrix then their matrix product AB is the m -by- p matrix whose entries are given by dot product of the corresponding row of A and the.
It is a very important step. AB AB do matrix multiplication if applicable. But its confusing that a left-multiplication transformation is defined using a matrix and need the idea of matrix multiplication.
We can augment a 33 matrix with the identity on the right and use row operations to turn the original matrix into the identity and the matrix on the right becomes the inverse. XA x you need to swap the second and third row. Representing the columns of X by colorful boxes will help visualize this.
As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. A matrix with 2 columns can be multiplied by any matrix with 2 rows.
Using parentheses to clarify the previous statement is exactly equivalent to the following.
Matrix Multiplication Chilimath
Properties Of Matrix Multiplication Article Khan Academy
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Introduction To Matrices And Vectors Multiplication Using Python Numpy
Dynamic Programming Deep Dive Chain Matrix Multiplication
How To Multiply Two Matrices Together Studypug
Finding The Product Of Two Matrices College Algebra
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
How To Multiply Two Matrices Together Studypug
Matrix By Matrix Multiplication
How To Multiply Matrices
15 3 Matrix Multiplication Chemistry Libretexts
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Matrix Multiplication And Linear Combinations
Matrix Multiplication Calculator
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Multiplying Matrices By Scalars Article Khan Academy
4 Multiplication Of Matrices
Matrix Multiplication And Linear Combinations
