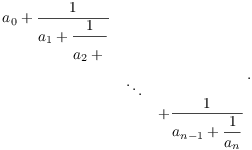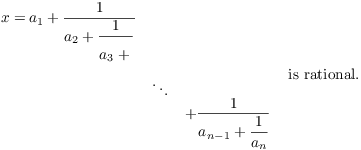Matrix Multiplication Continued Fractions
From this point on we suppose that 7. Hence if you want to divide a matrix by a scalar simply multiply the matrix by the reciprocal of your divider or just divide its the same thing.
While n 0 Continued fraction recurrence relations.

Matrix multiplication continued fractions. The theory of continued fractions is less widely known than it should be. If a 1 0 then remove this term otherwise insert 0 at the beginning of the sequence. A nonterminating matrix-valued continued fraction 21 is called convergent if the sequence Rn of approximants is convergent that is lim n R n lim n P n 0 Q n 0 lim n P n Q n R and the matrix R is taken as the value of the matrix-valued continued fraction.
P0 p1 q1 1. W 0 2 4 1 2 1 6. Continued Fractions and Matrices 1 Mn1 AnMn From Lemma 1 above 2 Applying Lemma 1 again gives us.
Satisfies the conditions of Proposition 3 and there is a unique decomposition correspond-ing to a continued fraction with admissible partial quotients. Algorithms for Continued Fractions Representing numbers is half the problem. R0 q0 q1.
For these tasks continued fractions will be of the form. Digit if r1 p1 r1- q1. We must also devise efficient algorithms for computing on them.
Now these are the steps. A 1 a 2. Handle first term here.
Bill Gosper has invented an algorithm for performing analytic addition subtraction multiplication and division using continued fractions. R0 p0 p1. If r1.
It is not yet considered ready to be promoted as a complete task for reasons that should be found in its talk page. A 0 1 a 1 1 a 2 1 a 3 displaystyle a_0cfrac 1a_1cfrac 1a_2cfrac 1a_3ddots so each may be described by the notation a 0. FD or 7 a l ZD2 with a positive integer 1 mod 4 and not.
A 1 2 a and b 1 1 1 2 b. You can find that. While digit 9 r0.
Many definitions and examples. Matrix B left number of columns 3. Since this is the case then it is okay to multiply them together.
Continued fractionArithmeticG matrix ng continued fraction n is a draft programming task. Inverting a continued fraction is trivial. Also the multiplicative inverse and the division of the simple continued fractions are showed.
Also given that that a b 2 b 6 3 a 2 b a b. Let 2 1 a and 3 1 b meaning that given the continued fractions of both 2 and 3 we have. Matrix E right number of rows 3.
It requires keeping track of eight integers which are conceptually arranged at the polyhedron vertices of a cube. Mn1 AnAn-1Mn-1 3 Since n is an integer greater than 0 we can keep on doing this until eventually we get. This task investigates mathmatical operations that can be performed on a single continued fraction.
These matrix continued fractions MCFs are generalisations of ordinary continued fractions of generalized continued fractions or n -fractions see 3 and of the general n. V 0 1 2 w 2 4 1 With these two vectors the dot product is. Putchar digit 0.
A n displaystyle a_0a_1a_2a_n. Yet one canreadily retrieve its fundamental results with little more than the ability to multiply 22matrices. 6 1 a 1 b 1 a b a b.
The product of two fractions is found by multiplying the numerators and multiplying the denominators separately. So as you can see matrix multiplication is basically doing this for each row in the matrix thats why Sal mentioned it. Non-trivial matrix actions preserve normality for continued fractions - Volume 153 Issue 2.
Longer answer - You can view scalar division as multiplying by the reciprocal ie dividing a numbermatrix by a set number is the same as multiplying by 1number For example. Frac34 times frac27 frac3times 24times 7 frac628 frac314 after simplification. Multiplication of two simple continued fractions are discovered.
6 2 3 we obtain. Vectors can be thought of as matrices with just one row or column. The most important that we will do in this paper we exploring how the simple continued fractions can be used to calculate the numbers operations on roots.
E E to have a product the number of columns of left matrix B must equal the number of rows of right matrix E. Digit.
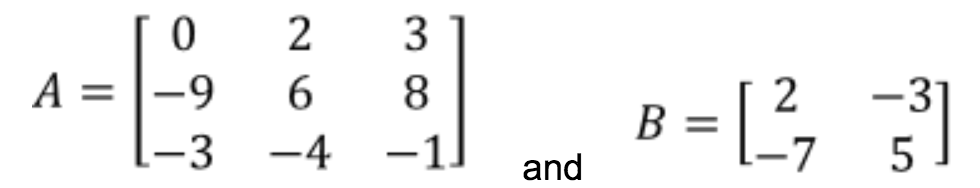
What Is An Identity Matrix Studypug

Intro To Lattices Continued Matrices The Liberated Mathematician
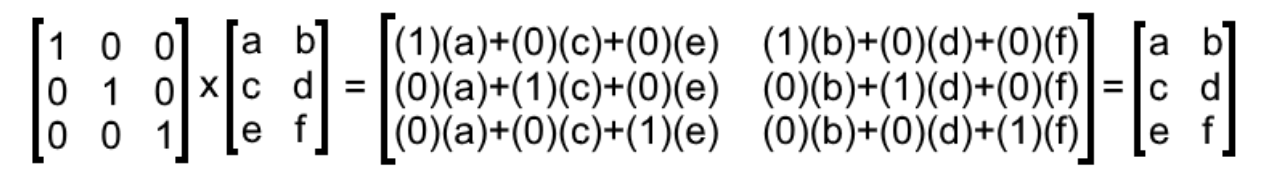
What Is An Identity Matrix Studypug

48 Questions With Answers In Matrix Theory Science Topic

Pin On Math Classroom Activities

Review Of Matrix Algebra Ppt Video Online Download

Review Of Matrix Algebra Ppt Video Online Download

48 Questions With Answers In Matrix Theory Science Topic

Review Of Matrix Algebra Ppt Video Online Download

Intro To Lattices Continued Matrices The Liberated Mathematician

Review Of Matrix Algebra Ppt Video Online Download